题目内容
在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,且点A(0,2),点C(![]() ,0),如下图所示;抛物线
,0),如下图所示;抛物线![]() 经过点B。
经过点B。
(1)求点B的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由。
解:(1)过点B作BD![]() 轴,垂足为D
轴,垂足为D
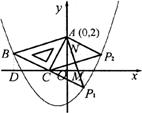
∵∠BCD+∠ACD=90°,∠ACO+∠OAC=90°
∴∠BCD=∠CAO
又∵∠BDC=∠COA=90°,CB=AC
∴△BCD≌△ACO
∴BD=OC=1,CD=OA=2
∴点B的坐标为(-3,1)
(2)抛物线![]() 经过点B(-3,1),则得
经过点B(-3,1),则得![]()
解得![]() ,所以抛物线解析式为
,所以抛物线解析式为![]()
(3)假设存在P、Q两点,使得△ACP是直角三角形:
①若以AC为直角边,点C为直角顶点;
则延长BC至点P1,使得P1C=BC,得到等腰直角三角形△ACP1
过点P1作P1M![]() 轴
轴
∵C P1=BC,∠MC P1=∠BCD,∠P1MC=∠BDC=90°
∴△M P1C≌△DBC
∴CM=CD=2,∴P1M=BD=1,可求得点P1(1,-1)
再证点P1在抛物线上
②若以AC为直角边,点A为直角顶点;
则过点A作AP2⊥CA,且使得A P2=AC,得到等腰直角三角形△AC P2
过点P2作P2N![]() ,同理可证△AP2N≌△CAO
,同理可证△AP2N≌△CAO
∴N P2=OA=2,AN=OC=1,可求得点P2(2,1)
再证点P2在抛物线上
当![]() 时,
时,![]()
当![]() 时,
时,![]()
所以,在抛物线上还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形。

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB= 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.