题目内容
【题目】如图,完成下列推理过程:
如图所示,点E在△ABC外部,点D在BC边上,DE交AC于F,若∠1=∠3,∠E=∠C,AE=AC,求证:△ABC≌△ADE.

证明:∵ ∠E=∠C(已知),
∠AFE=∠DFC(_________________),
∴∠2=∠3(______________________),
又∵∠1=∠3(_________________),
∴ ∠1=∠2(等量代换),
∴__________+∠DAC= __________+∠DAC(______________________),
即∠BAC =∠DAE,
在△ABC和△ADE中
∵ 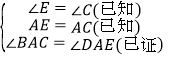
∴△ABC≌△ADE(_________________).
【答案】 对顶角相等 三角形内角和定理 已知 ∠1 ∠2 等式的性质 ASA
【解析】首先证明∠2=∠3,再证明∠BAC=∠DAE,进而可利用ASA判定三角形全等即可.
∵∠E=∠C(已知),
∠AFE=∠DFC(对顶角相等),
∴∠2=∠3(三角形内角和定理).
又∵∠1=∠3(已知),
∴∠1=∠2(等量代换),
∴∠1+∠DAC=∠2+∠DAC(等式的性质),
即∠BAC=∠DAE.
在△ABC和△ADE中,
∵ ,
,
∴△ABC≌△ADE(ASA).

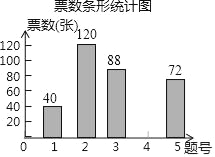
【题目】为提高三亚市初级中学教师业务水平,相关单位举办了首届“三亚市敏特杯数学命题大赛”,在众多自命题题目中共有5道题目进入专家组评审,将前5天的投票数据整理成如下不完整的统计图表:
票数条形统计图
题目编号 | 人数 | 百分比 |
1 | 40 | 10% |
2 | 120 | m% |
3 | 88 | 22% |
4 | a | 20% |
5 | 72 | 18% |
合计 | 400 | 1 |
请根据图表提供的信息,解答下面问题:
(1)票数统计表中的a= ,m= .
(2)请把票数统计图补充完整;
(3)若绘制“票数扇形统计图”编号是“4”的题目所对应扇形的圆心角是 度;
(4)至本次投票结束,总票数共有1200票,请估计编号是“3”的题目约获得 票.