题目内容
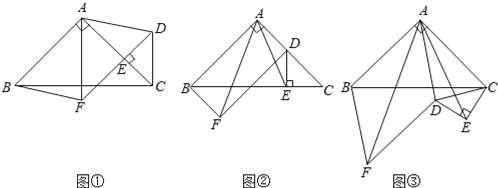
【题目】如图①,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合),在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系;
(2)①将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
②若AB=2![]() ,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
【答案】(1)AF= ![]() (2)结论:AF=
(2)结论:AF= ![]() (3)4
(3)4![]() 或2
或2![]()
【解析】试题(1)如图①中,只要证明△AEF是等腰直角三角形即可得到结论AF=![]() AE;
AE;
(2)如图②中,连接EF,DF交BC于K,先证明△EKF≌△EDA,再证明△AEF是等腰三角形即可;
(3)如图③中,连接EF,延长FD交AC于K,先证明△EDF≌△ECA,再证明△AEF是等腰直角三角形即可.
试题解析:(1)AF= ![]()
如图2,结论:AF= ![]()
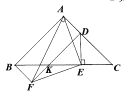
理由:连接EF,DF交BC于K,
∵四边形ABFD是平行四边形,∴AB∥DF,∴∠DKE=∠ABC=45°
∴∠EKF=180°=∠DKE=135°,
∵∠ADE=180°-∠EDC=180°-45°=135°,∴∠EKF=∠ADE,
∵∠DKG=∠C,∴DK=DC,
∵DF=AB=AC,∴KF=AD,
在△EKF和△EDA中,
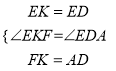
∴△EKF≌△EDA
∴EF=EA,∠KEF=∠AED,∴∠FEA=∠BED=90°,∴△AEF是等腰直角三角形,
∴AF=![]() AE
AE
(3)4![]() 或2
或2![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目