��Ŀ����
��ͼ��1������֪������ABCD��ֱ��MN���Ϸ���BC��ֱ��MN�ϣ�E������BC��һ�㣬��AEΪ����ֱ��MN���Ϸ���������AEFG��
��1������FC���۲첢�²��FCN�Ķ�������˵�����ɣ�
��2����ͼ��2������ͼ��1����������ABCD��Ϊ����ABCD��AB=m��BC=n��m��nΪ��������E���߶�BC��һ���㣨�����˵�B��C������AEΪ����ֱ��MN���Ϸ�������AEFG��ʹ����Gǡ����������CD�ϣ�����E������CN�˶�ʱ�����ú�m��n�Ĵ���ʽ��ʾtan��FCN��ֵ��
��1������FC���۲첢�²��FCN�Ķ�������˵�����ɣ�
��2����ͼ��2������ͼ��1����������ABCD��Ϊ����ABCD��AB=m��BC=n��m��nΪ��������E���߶�BC��һ���㣨�����˵�B��C������AEΪ����ֱ��MN���Ϸ�������AEFG��ʹ����Gǡ����������CD�ϣ�����E������CN�˶�ʱ�����ú�m��n�Ĵ���ʽ��ʾtan��FCN��ֵ��

���㣺�ı����ۺ���
ר�⣺�����ۺ���,���ν��
��������1�����������ε��������ȵó���FEH=��BAE�����ɵó���EHF�ա�ABE��AAS���������FCN�Ķ������ɣ�
��2�����þ��ε����ʵó��Լ�ȫ�������ε��ж������ʺ����������ε��ж������ʵó���EFH�ա�AGD����EFH�ס�AEB�����ɵó�tan��FCN=
=
=
��
��2�����þ��ε����ʵó��Լ�ȫ�������ε��ж������ʺ����������ε��ж������ʵó���EFH�ա�AGD����EFH�ס�AEB�����ɵó�tan��FCN=
| FH |
| CH |
| EH |
| AB |
| n |
| m |
����⣺��1����FCN=45�㣬
�����ǣ���FH��MN��H��
�ߡ�AEF=��ABE=90�㣬
���BAE+��AEB=90�㣬��FEH+��AEB=90�㣬
���FEH=��BAE��
�ڡ�EHF�͡�ABE��
��
���EHF�ա�ABE��AAS����
��FH=BE��EH=AB=BC��
��CH=BE=FH��
�ߡ�FHC=90�㣬
���FCH=45�㣻
��2����ͼ��2����FH��MN��H��
����֪�ɵá�EAG=��BAD=��AEF=90�㣬
��ϣ�1���á�FEH=��BAE=��DAG��
�֡�G������CD�ϣ�
��GDA=��EHF=��EBA=90�㣬
�ڡ�EFH�͡�AGD��
��
���EFH�ա�AGD��AAS����
�ߡ�BAE=��FEH����ABE=��FHE��
���EFH�ס�AEB��
��EH=AD=BC=n����CH=BE��
��
=
=
��
����Rt��FEH��tan��FCN=
=
=
��
�൱��E������CN�˶�ʱ��tan��FCN=
��
�����ǣ���FH��MN��H��
�ߡ�AEF=��ABE=90�㣬
���BAE+��AEB=90�㣬��FEH+��AEB=90�㣬
���FEH=��BAE��
�ڡ�EHF�͡�ABE��
|
���EHF�ա�ABE��AAS����
��FH=BE��EH=AB=BC��
��CH=BE=FH��
�ߡ�FHC=90�㣬
���FCH=45�㣻
��2����ͼ��2����FH��MN��H��
����֪�ɵá�EAG=��BAD=��AEF=90�㣬

��ϣ�1���á�FEH=��BAE=��DAG��
�֡�G������CD�ϣ�
��GDA=��EHF=��EBA=90�㣬
�ڡ�EFH�͡�AGD��
|
���EFH�ա�AGD��AAS����
�ߡ�BAE=��FEH����ABE=��FHE��
���EFH�ס�AEB��
��EH=AD=BC=n����CH=BE��
��
| EH |
| AB |
| FH |
| BE |
| FH |
| CH |
����Rt��FEH��tan��FCN=
| FH |
| CH |
| EH |
| AB |
| n |
| m |
�൱��E������CN�˶�ʱ��tan��FCN=
| n |
| m |
������������Ҫ�������ı����ۺ��Լ�ȫ�������ε��ж��������Լ������κ;��ε����ʵ�֪ʶ��ע�����ν�ϵó�ȫ���������ǽ���ؼ���

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ��BE��BD�ǡ�ABC�С�ABC���ڡ����ƽ���ߣ�AD��BD��D��AE��BE��E����BC���ӳ�����F��
��ͼ��BE��BD�ǡ�ABC�С�ABC���ڡ����ƽ���ߣ�AD��BD��D��AE��BE��E����BC���ӳ�����F�� ��ͼ���ı���ABCD�������Σ���G��BC������һ�㣬BE��AG�ڵ�E����FΪAE��һ�㣬��AE-BE=EF����֤��BE��DF��
��ͼ���ı���ABCD�������Σ���G��BC������һ�㣬BE��AG�ڵ�E����FΪAE��һ�㣬��AE-BE=EF����֤��BE��DF�� ��ͼ��һ�һ����ɸۿ�A����������������ʻ���ڸۿ�A��ʱ����õ���B�ڸۿ�A����ƫ��30�㷽��С��C�ڸۿ�A����ƫ��60�㷽�����һ�����ʻ60���ﵽ��D��ʱ��С��Cǡ���ڵ�D�������Ϸ���ʱ��õ���B����ƫ��60��ķ�����
��ͼ��һ�һ����ɸۿ�A����������������ʻ���ڸۿ�A��ʱ����õ���B�ڸۿ�A����ƫ��30�㷽��С��C�ڸۿ�A����ƫ��60�㷽�����һ�����ʻ60���ﵽ��D��ʱ��С��Cǡ���ڵ�D�������Ϸ���ʱ��õ���B����ƫ��60��ķ�����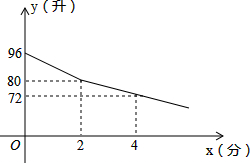 ijУ����סУ������ѧ��ѧУ��¯����ˮ��ÿ�˽�ˮ2����������ͬʱ��������ˮ��ͷ����������Ϲر�һ����ˮ��ͷ������ǰ�����˽�ˮ���ʱ����Բ��ƣ��Ҳ�������������¯�ڵ���ˮ��y���������ˮʱ��x���֣��ĺ���ͼ����ͼ������ͼ�ش��������⣺
ijУ����סУ������ѧ��ѧУ��¯����ˮ��ÿ�˽�ˮ2����������ͬʱ��������ˮ��ͷ����������Ϲر�һ����ˮ��ͷ������ǰ�����˽�ˮ���ʱ����Բ��ƣ��Ҳ�������������¯�ڵ���ˮ��y���������ˮʱ��x���֣��ĺ���ͼ����ͼ������ͼ�ش��������⣺