题目内容
 如图,四边形ABCD是正方形,点G是BC上任意一点,BE⊥AG于点E,点F为AE上一点,且AE-BE=EF,求证:BE∥DF.
如图,四边形ABCD是正方形,点G是BC上任意一点,BE⊥AG于点E,点F为AE上一点,且AE-BE=EF,求证:BE∥DF.考点:全等三角形的判定与性质,正方形的性质
专题:证明题
分析:求出AD=AB,AF=BE,∠DAF=∠ABE,推出△ADF≌△BEA,求出∠DFE=∠BEA=90°,根据平行线的判定推出即可.
解答:证明:∵四边形ABCD是正方形,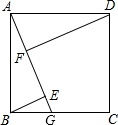
∴AD=AB,∠ABG=90°,AD∥BC,
∴∠FAD=∠AMB,
∵BE⊥AG,
∴∠AEB=∠BEG=90°=∠ABG,
∴∠ABE+∠GBE=90°,∠AGB+∠EBG=90°,
∴∠ABE=∠BGA=∠DAF,
∵AE-BE=EF,AE-AF=EF,
∴AF=BE,
在△ADF和△BEA中,
∴△ADF≌△BEA(SAS),
∴∠AFD=∠BEA=90°,
∴∠DFE=∠BEA=90°,
∴BE∥DF.

∴AD=AB,∠ABG=90°,AD∥BC,
∴∠FAD=∠AMB,
∵BE⊥AG,
∴∠AEB=∠BEG=90°=∠ABG,
∴∠ABE+∠GBE=90°,∠AGB+∠EBG=90°,
∴∠ABE=∠BGA=∠DAF,
∵AE-BE=EF,AE-AF=EF,
∴AF=BE,
在△ADF和△BEA中,
|
∴△ADF≌△BEA(SAS),
∴∠AFD=∠BEA=90°,
∴∠DFE=∠BEA=90°,
∴BE∥DF.
点评:本题考查了正方形的性质,全等三角形的性质和判定,平行线的判定的应用,能推出△ADF≌△BEA是解此题的关键,注意:全等三角形的对应角相等.

练习册系列答案
相关题目
 如图,直线AP的解析式y=kx+4k分别交于x轴、y轴于A、C两点,与反比例函数y=
如图,直线AP的解析式y=kx+4k分别交于x轴、y轴于A、C两点,与反比例函数y=
 如图,在△ABC中,cosB=
如图,在△ABC中,cosB= 已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-2,0)、B(x1,0),且1<x1<2,与y轴正半轴的交点在(0,2)的上方,顶点为C.直线y=kx+m(k≠0)经过点C、B.则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-2,0)、B(x1,0),且1<x1<2,与y轴正半轴的交点在(0,2)的上方,顶点为C.直线y=kx+m(k≠0)经过点C、B.则下列结论: