��Ŀ����
����Ŀ�����壺���㡢���ڴ�С��ͬ�����ڷ����෴���������κ�����Ϊ�����ض��κ�������
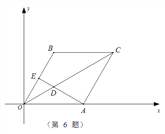
��1����֪���κ���y=��(x��2)2��3�������ġ����ض��κ�������__________________��
��2����֪����x�Ķ��κ���y1=2x2��2mx��m+1��y2=ax2+bx��c������y1��ͼ���㣨1��1��.��y1��y2��y1��Ϊ�����ض��κ�����.����y2�ı���ʽ����ֱ��д����0��x��3ʱ��y2����Сֵ��
���𰸡�(1)��y=��x��2��2+3��(2)����16��
��������������(1)�����ݡ����ض��κ������Ķ���ó��𰸣�(2)������y1��ͼ����A��1,1�����m��ֵ��Ȼ��ó�y1+y2�ĺ�������ʽ�����ݡ����ض��κ������Ķ���ó�a��b��c��ֵ���Ӷ��ó�y2�ĺ�������ʽ�����ݶ��κ��������ʵó���Сֵ��
��⣺��1��y=��x��2��2+3
��2����y1��ͼ����A��1,1���� ��2��2m+m+2=2�� ���m=2��
��y1=2x2��4x+3=2��x��1��2+1�� ��y1+y2=2x2��4x+3+ax2+bx+c=��a+2��x2+��b��4��x+c+3��
��y1+y2��y1Ϊ�����ض��κ������� ��y1+y2=-2��x��1��2+1=��2x2+4x��1��
��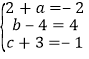 �����
�����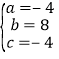 �� �ຯ��y2�ı���ʽΪ��y2=��4x2+8x��4��
�� �ຯ��y2�ı���ʽΪ��y2=��4x2+8x��4��
��0��x��3ʱ��y2����СֵΪ��16��

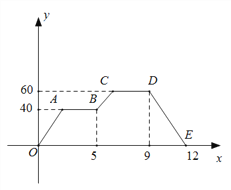
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ij�д�![]() ��
��![]() ��
��![]() �տ�ʼʵʩ���ݵ���ƣ����������õ�۸����£�
�տ�ʼʵʩ���ݵ���ƣ����������õ�۸����£�
���� | ���õ��� | ��� ����λ��Ԫ | |
���^�� | ���ļ��� | ||
�� | ������ | ������ |
|
�� | ���� | ���� |
|
�� | ���� | ���� |
|
������ij�û�![]() ��
��![]() �µ��õ���Ϊ
�µ��õ���Ϊ![]() �ȣ����轻���Ϊ��
�ȣ����轻���Ϊ��
![]() ��Ԫ����
��Ԫ����
��1��������![]() ��
��![]() �µ��õ���Ϊ
�µ��õ���Ϊ![]() �ȣ����轻��Ѷ���Ԫ��
�ȣ����轻��Ѷ���Ԫ��
��2��������![]() ��
��![]() �º�
�º�![]() ���õ�����ͬ���������
���õ�����ͬ���������![]() Ԫ����С����
Ԫ����С����![]() �·��ö��ٶȵ磿
�·��ö��ٶȵ磿