Question

【题目】已知等边△ABC中，点D为射线BA上一点，作DE=DC，交直线BC于点E,∠ABC的平分线BF交CD于点F，过点A作AH⊥CD于H，当EDC=30 ，CF= ，则DH= ．

Answer 1

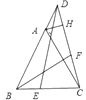
【答案】
【解析】连接AF.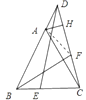

∵△ABC是等边三角形，
∴AB=BC，∠ABC=∠ACB=∠BAC=60°.
∵DE=DC，∠EDC=30°，
∴∠DEC=∠DCE=75°，
∴∠ACF=75°-60°=15°.
∵BF平分∠ABC，
∴∠ABF=∠CBF.
在△ABF和△CBF中， ，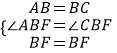
∴△ABF≌△CBF，
∴AF=CF，
∴∠FAC=∠ACF=15°，
∴∠AFH=15°+15°=30°.
∵AH⊥CD，
∴AH= AF= CF= .
∵∠DEC=∠ABC+∠BDE，
∴∠BDE=75°-60°=15°，
∴∠ADH=15°+30°=45°，
∴∠DAH=∠ADH=45°，
∴DH=AH= .
故答案为： .
连接AF.根据等边三角形的性质得出AB=BC，∠ABC=∠ACB=∠BAC=60° ，根据等腰三角形的性质得出∠DEC=∠DCE=75° ，根据角的和差得出∠ACF=75°-60°=15°.根据角平分线的定义得出∠ABF=∠CBF ，从而利用SAS判断出△ABF≌△CBF，根据全等三角形的性质得出AF=CF，进而∠FAC=∠ACF=15°，根据三角形的外角性质得出∠AFH=15°+15°=30°.根据含30°角的直角三角形的边之间的关系得出AH= AF= CF= .然后根据角的和差得出∠DAH=∠ADH=45°，从而得出DH的长度。