题目内容
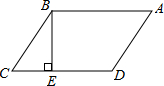
如图，平行四边形ABCD中，E是BC上一点，延长DE、AB交于点F，若BE：BC=1：3，CD=4，则AF长为______．
证明：在?ABCD中，∵AD∥BC，
∴∠EBF=∠A，∠ADF=∠BEF，
又∵∠F=∠F，
∴△BEF∽△ADF，
∴
=
，
设BF的长度为x，则AF=4+x，
代入得：
=
解得：x=2，
故AF=6．
故答案为：6．
∴∠EBF=∠A，∠ADF=∠BEF，
又∵∠F=∠F，
∴△BEF∽△ADF，
∴
| BE |
| AD |
| BF |
| AF |
设BF的长度为x，则AF=4+x，
代入得：
| 1 |
| 3 |
| x |
| 4+x |
解得：x=2，
故AF=6．
故答案为：6．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
