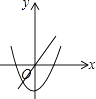题目内容
【题目】已知抛物线 y= ![]() x2﹣2x的顶点是A,与x轴相交于点B、C两点(点B在点C的左侧).
x2﹣2x的顶点是A,与x轴相交于点B、C两点(点B在点C的左侧).
(1)求A、B、C的坐标;
(2)直接写出当y<0时x的取值范围.
【答案】
(1)解:y= ![]() x2﹣2x=
x2﹣2x= ![]() (x2﹣4x+4)﹣2=
(x2﹣4x+4)﹣2= ![]() (x﹣2)2﹣2,
(x﹣2)2﹣2,
则函数的顶点坐标是(2,﹣2),
即A的坐标是(2,﹣2).
令y=0,则 ![]() x2﹣2x=0,
x2﹣2x=0,
解得x=0或4,
则B的坐标是(0,0),C的坐标是(4,0)
(2)解:x的范围是0<x<4.
【解析】(1)利用配方法即可确定函数的顶点坐标;令y=0,解方程即可求得与x轴的交点的横坐标;(2)y<0求x的范围,根据函数开口向上,以及函数与x轴的交点即可确定.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.

练习册系列答案
相关题目
【题目】某茶叶厂用甲,乙,丙三台包装机分装质量为200g的茶叶,从它们各自分装的茶叶中分别随机抽取了20盒,得到它们的实际质量的方差如下表所示:
甲包装机 | 乙包装机 | 丙包装机 | |
方差 | 10.96 | 5.96 | 12.32 |
根据表中数据,可以认为三台包装机中,包装茶叶的质量最稳定是_____.