题目内容
【题目】如图,直角△ABC内接于⊙O,点D是直角△ABC斜边AB上的一点,过点D作AB的垂线交AC于E,过点C作∠ECP=∠AED,CP交DE的延长线于点P,连结PO交⊙O于点F.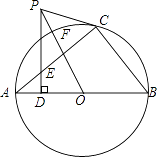
(1)求证:PC是⊙O的切线;
(2)若PC=3,PF=1,求AB的长.
【答案】
(1)解:如图,连接OC,
∵PD⊥AB,
∴∠ADE=90°,
∵∠ECP=∠AED,
又∵∠EAD=∠ACO,
∴∠PCO=∠ECP+∠ACO=∠AED+∠EAD=90°,
∴PC⊥OC,
∴PC是⊙O切线
(2)解:解法一:
延长PO交圆于G点,
∵PF×PG=PC2,PC=3,PF=1,
∴PG=9,
∴FG=9﹣1=8,
∴AB=FG=8.
解法二:
设⊙O的半径为x,则OC=x,OP=1+x
∵PC=3,且OC⊥PC
∴32+x2=(1+x)2
解得x=4
∴AB=2x=8
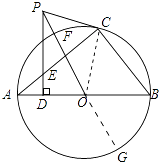
【解析】(1)连接OC,欲证明PC是⊙O的切线,只要证明PC⊥OC即可.(2)延长PO交圆于G点,由切割线定理求出PG即可解决问题.

练习册系列答案
相关题目