题目内容
5.在△ABC中,∠A=50°,若点O是△ABC的内心,则∠BOC=115°.分析 利用三角形的内心的性质得出∠ABO+∠ACO=∠OBC+∠OCB=65°,进而得出答案.
解答 解:如图所示: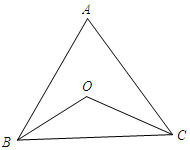
∵∠A=50°,
∴∠ABC+∠BCA=130°.
∵O是△ABC的内心,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB.
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠BCA)=65°.
∴∠BOC=180°-65°=115°.
点评 此题主要考查了三角形内心的性质以及三角形内角和定理,根据已知得出∠ABO+∠ACO=∠OBC+∠OCB=65°是解题关键

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 在平行四边形ABCD中,E,F分别是AB,CD的中点,求证:四边形EBFD是平行四边形.
在平行四边形ABCD中,E,F分别是AB,CD的中点,求证:四边形EBFD是平行四边形.