题目内容
 已知:如图,点B在y轴的负半轴上,点A在x轴的正半轴上,且OA=2,tan∠OAB=2.
已知:如图,点B在y轴的负半轴上,点A在x轴的正半轴上,且OA=2,tan∠OAB=2.(1)求点B的坐标;
(2)求直线AB的解析式;
(3)若点C的坐标为(-2,0),在直线AB上是否存在一点P,使△APC与△AOB相似?若存在,求出点P的坐标;若不存在,请说明理由.
分析:(1)由已知数据求出OB的长即可求出B的坐标;
(2)设直线AB的解析式为y=kx+b(k≠0),把A(2,0)和B(0,-4)的坐标代入求出k和b的值即可求出直线AB的解析式;
(3)在直线AB上是否存在一点P,使△APC与△AOB相似,过C作P1C∥OB交AB于P1,这时△APC与△AOB相似,过C作P2C⊥AB交AB于P2,过P2作P1D⊥AC于D,则△AOB∽△ACP2,有相似三角形的性质即可求出符合题意的点P的坐标.
(2)设直线AB的解析式为y=kx+b(k≠0),把A(2,0)和B(0,-4)的坐标代入求出k和b的值即可求出直线AB的解析式;
(3)在直线AB上是否存在一点P,使△APC与△AOB相似,过C作P1C∥OB交AB于P1,这时△APC与△AOB相似,过C作P2C⊥AB交AB于P2,过P2作P1D⊥AC于D,则△AOB∽△ACP2,有相似三角形的性质即可求出符合题意的点P的坐标.
解答:解:(1)在Rt△ABC中,
tan∠OAB=
,
∵OA=2,tan∠OAB=2,
∴OB=4,
∵点B在y轴的负半轴上,
∴B(0,-4),
(2)∵OA=2,
∴A(2,0),
设直线AB的解析式为y=kx+b(k≠0),
则
,
∴
,
∴直线AB的解析式为y=2x-4;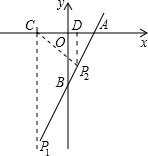
(3)过C作P1C∥OB交AB于P1
这时△APC与△AOB相似,
当x=-2时,y=-8,
则P1(-2,-8),
过C作P2C⊥AB交AB于P2,过P2作P1D⊥AC于D,
由△AOB∽△ACP2,求出AP2=
,
由△AOB∽△ADP2,求出AD=
,
则OD=
,
当x=
时,y=-
,
则P1(
,-
),
存在点P1(-2,-8)或(
,-
),使△APC与△AOB相似.
tan∠OAB=
| OB |
| OA |
∵OA=2,tan∠OAB=2,
∴OB=4,
∵点B在y轴的负半轴上,
∴B(0,-4),
(2)∵OA=2,
∴A(2,0),
设直线AB的解析式为y=kx+b(k≠0),
则
|
∴
|
∴直线AB的解析式为y=2x-4;

(3)过C作P1C∥OB交AB于P1
这时△APC与△AOB相似,
当x=-2时,y=-8,
则P1(-2,-8),
过C作P2C⊥AB交AB于P2,过P2作P1D⊥AC于D,
由△AOB∽△ACP2,求出AP2=
4
| ||
| 5 |
由△AOB∽△ADP2,求出AD=
| 4 |
| 5 |
则OD=
| 6 |
| 5 |
当x=
| 6 |
| 5 |
| 8 |
| 5 |
则P1(
| 6 |
| 5 |
| 8 |
| 5 |
存在点P1(-2,-8)或(
| 6 |
| 5 |
| 8 |
| 5 |
点评:本题考查了锐角三角函数值的运用、用待定系数法求一次函数的解析式以及相似三角形的判定和性质,题目的综合性强,难度大,解题的时要注意分类讨论的数学思想的运用.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 (1998•南京)已知:如图,点P在∠AOB的边OA上.
(1998•南京)已知:如图,点P在∠AOB的边OA上. 已知:如图,点C在BE上,AB∥ED,AB=CE,BC=ED.
已知:如图,点C在BE上,AB∥ED,AB=CE,BC=ED. 已知:如图,点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.求证:BD=CE.
已知:如图,点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.求证:BD=CE. 已知,如图,点F在AB上,点E在CD上,AE、DF分别交BC于H、G,∠A=∠D,∠FGB+∠EHG=180°,问AB与CD有怎样的位置关系?为什么?
已知,如图,点F在AB上,点E在CD上,AE、DF分别交BC于H、G,∠A=∠D,∠FGB+∠EHG=180°,问AB与CD有怎样的位置关系?为什么? (1)已知:如图,点C在线段AB上,AC=18cm,BC=6cm,点M、N分别是AC、BC的中点,求MN的长;
(1)已知:如图,点C在线段AB上,AC=18cm,BC=6cm,点M、N分别是AC、BC的中点,求MN的长;