Question

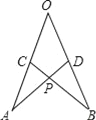
【题目】如图所示，在∠AOB的两边上截取AO=BO，CO=DO，连接AD、BC交于点P，则①△AOD≌△BOC；②△APC≌△BPD；③P在∠AOB的平分线上，其中结论正确的是（　　）

A. ① B. ② C. ①② D. ①②③

Answer 1

【答案】D

【解析】由AO=BO，∠O=∠O，DO=CO，①△AOD≌△BOC，∠A=∠B；AO=BO，CO=DOAC=BD，又∠A=∠B，∠APC=BPD②△APC≌△BPD；连接OP，容易证明△AOP≌△BOP∠AOP=∠BOP③点P在∠AOB的平分线上．

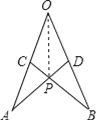
解：连接OP，

在△AOD和△BOC中，

AO=BO，∠O=∠O，DO=CO，

∴△AOD≌△BOC（SAS），故①正确；

∴∠A=∠B；

∵AO=BO，CO=DO，

∴AC=BD，

在△APC和△BPD中，

∠A=∠B，∠APC=∠BPD，AC=BD，

∴△APC≌△BPD（AAS），故②正确；

∴AP=BP，

在△AOP和△BOP中，

AP=BP，AO=BO，OP=OP，

∴△AOP≌△BOP（SSS），

∴∠AOP=∠BOP，即点P在∠AOB的平分线上，故③正确．

故选D．

“点睛”本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、AAS、ASA和HL，做题时，要根据已知条件结合图形进行思考.