Question

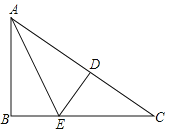
【题目】如图,在△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在边AC上,与点B′重合,AE为折痕，则EB=_____________.

Answer 1

【答案】1.5．

【解析】首先根据折叠可得BE=EB′，AB′=AB=3，然后设BE=EB′=x，则EC=4-x，在Rt△ABC中，由勾股定理求得AC的值，再在Rt△B′EC中，由勾股定理可得方程x2+22=（4-x）2，再解方程即可算出答案．

解：根据折叠可得BE=EB′，AB′=AB=3，
设BE=EB′=x，则EC=4-x，
∵∠B=90°，AB=3，BC=4，
∴在Rt△ABC中，由勾股定理得，AC==5，
∴B′C=5-3=2，
在Rt△B′EC中，由勾股定理得，x2+22=（4-x）2，
解得x=1.5，
故答案为：1.5．