题目内容
“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程 的两根,且a < b, 则a、b、m、n 的大小关系是( )
的两根,且a < b, 则a、b、m、n 的大小关系是( )
| A.m < a < b< n | B.a < m < n < b | C.a < m < b< n | D.m < a < n < b |
A
解析试题分析:类比“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”这句话,可以得出:若m、n(m<n)是关于x的方程 的两根,则二次函数
的两根,则二次函数 的图象与直线
的图象与直线 有两个公共点,于是根据图象:
有两个公共点,于是根据图象:
可知:m < a < b< n,故选A.
考点:二次函数图象与系数的关系.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
将二次函数y=x2的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是
| A.y=(x–1)2+2 | B.y=(x+1)2+2 |
| C.y=(x–1)2–2 | D.y=(x+1)2–2 |
如图,已知点A1,A2,…,A2011在函数 位于第二象限的图象上,点B1,B2,…,B2011在函数
位于第二象限的图象上,点B1,B2,…,B2011在函数 位于第一象限的图象上,点C1,C2,…,C2011在y轴的正半轴上,若四边形
位于第一象限的图象上,点C1,C2,…,C2011在y轴的正半轴上,若四边形 、
、 ,…,
,…, 都是正方形,则正方形
都是正方形,则正方形 的边长为
的边长为
| A.2010 | B.2011 | C.2010 | D.2011 |
抛物线y=-x2+2x+3的顶点坐标是( )
| A.(-1,4) | B.(1,3) | C.(-1,3) | D.(1,4) |
甲、乙两位同学对问题“求代数式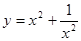 的最小值”提出各自的想法.甲说:“可以利用已经学过的完全平方公式,把它配方成
的最小值”提出各自的想法.甲说:“可以利用已经学过的完全平方公式,把它配方成 ,所以代数式的最小值为-2”.乙说:“我也用配方法,但我配成
,所以代数式的最小值为-2”.乙说:“我也用配方法,但我配成 ,最小值为2”.你认为( )
,最小值为2”.你认为( )
| A.甲对 | B.乙对 | C.甲、乙都对 | D.甲乙都不对 |
抛物线y=3x2,y=-3x2,y= x2+3共有的性质是
x2+3共有的性质是
| A.开口向上 | B.对称轴是y轴 |
| C.都有最高点 | D.y随x值的增大而增大 |

 经过平移得到抛物线
经过平移得到抛物线 ,其对称轴与两段抛物线所围成的阴影部分的面积为( )
,其对称轴与两段抛物线所围成的阴影部分的面积为( )




