题目内容
如图,抛物线![]() 与
与![]() 轴交于A、B两点(点A在点B左侧),与y轴交
轴交于A、B两点(点A在点B左侧),与y轴交
于点C,且当![]() =0和
=0和![]() =4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。
=4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。
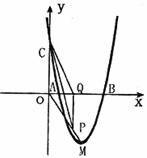
(1)求这条抛物线的解析式;
(2)P为线段OM上一点,过点P作PQ⊥![]() 轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
(3)随着点P的运动,四边形PQCO的面积S有最大值吗?如果S有最大值,请求出S的最大值并指出点Q的具体位置和四边形PQCO的特殊形状;如果S没有最大值,请简要说明理由;
(4)随着点P的运动,是否存在t的某个值,能满足PO=OC?如果存在,请求出t的值。
解:(1)∵当![]() 和
和![]() 时,
时,![]() 的值相等,∴
的值相等,∴![]() ,
,
∴![]() ,∴
,∴![]()
将![]() 代入
代入![]() ,得
,得![]() ,
,
将![]() 代入
代入![]() ,得
,得![]()
∴设抛物线的解析式为![]()
将点![]() 代入,得
代入,得![]() ,解得
,解得![]() .
.
∴抛物线![]() ,即
,即![]()
(2)设直线OM的解析式为![]() ,将点M
,将点M![]() 代入,得
代入,得![]() ,
,
∴![]()
则点P![]() ,
,![]() ,而
,而![]() ,
,![]() .
.
![]() =
=![]()
![]() 的取值范围为:
的取值范围为:![]() <
<![]() ≤
≤![]()
(3)随着点![]() 的运动,四边形
的运动,四边形![]() 的面积
的面积![]() 有最大值.
有最大值.
从图像可看出,随着点![]() 由
由![]() →
→![]() 运动,
运动,![]() 的面积与
的面积与![]() 的面积在不断增大,即
的面积在不断增大,即![]() 不断变大,当然点
不断变大,当然点![]() 运动到点
运动到点![]() 时,
时,![]() 最值
最值
此时![]() 时,点
时,点![]() 在线段
在线段![]() 的中点上
的中点上
因而![]() .
.
当![]() 时,
时,![]() ,
,![]() ∥
∥![]() ,∴四边形
,∴四边形![]() 是平行四边形.
是平行四边形.
(4)随着点![]() 的运动,存在
的运动,存在![]() ,能满足
,能满足![]()
设点![]() ,
,![]() ,
,![]() . 由勾股定理,得
. 由勾股定理,得![]() .
.
∵![]() ,∴
,∴![]() ,
,![]() <
<![]() ,
,![]() (不合题意)
(不合题意)
∴当![]() 时,
时,![]()

练习册系列答案
相关题目
 轴交于
轴交于 (2)点
(2)点 为抛物线上一动点,在
为抛物线上一动点,在 ,使以
,使以 与
与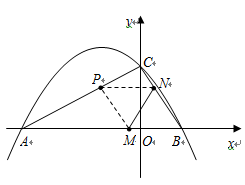
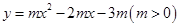 与
与 轴交于
轴交于 两点,与
两点,与 轴交于
轴交于 点.
点.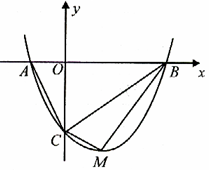
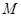 的坐标(用含
的坐标(用含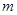 的代数式表示),
的代数式表示), 与
与 的面积比不变,试求出这个比值;
的面积比不变,试求出这个比值;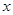 轴交于
轴交于 (
( ,0)、
,0)、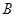 (
( ,0)两点,且
,0)两点,且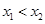 ,与
,与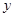 轴交于点
轴交于点 ,其中
,其中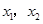 是方程
是方程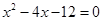 的两个根。(14分)
的两个根。(14分) (2)点
(2)点 是线段
是线段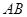 上的一个动点,过点
上的一个动点,过点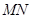 ∥
∥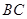 ,交
,交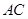 于点
于点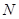 ,连接
,连接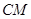 ,当
,当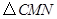 的面积最大时,求点
的面积最大时,求点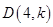 在(1)中抛物线上,
在(1)中抛物线上,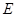 为抛物线上一动点,在
为抛物线上一动点,在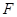 ,使以
,使以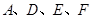 为顶
为顶