题目内容
 如图∠BOP=∠AOP=15°,PC∥OB,PD⊥PB于D,PC=2,则PD的长度为( )
如图∠BOP=∠AOP=15°,PC∥OB,PD⊥PB于D,PC=2,则PD的长度为( )| A、4 | B、3 | C、2 | D、1 |
分析:作PE⊥OA于E,根据角平分线的性质可得PE=PD,根据平行线的性质可得∠ACP=∠AOB=30°,由直角三角形中30°的角所对的直角边等于斜边的一半,可求得PE,即可求得PD.
解答: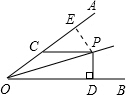 解:作PE⊥OA于E,
解:作PE⊥OA于E,
∵∠AOP=∠BOP,PD⊥OB,PE⊥OA,
∴PE=PD(角平分线上的点到角两边的距离相等),
∵∠BOP=∠AOP=15°,
∴∠AOB=30°,
∵PC∥OB,
∴∠ACP=∠AOB=30°,
∴在Rt△PCE中,PE=
PC=
×2=1(在直角三角形中,30°角所对的直角边等于斜边的一半),
∴PD=PE=1,
故选D.
 解:作PE⊥OA于E,
解:作PE⊥OA于E,∵∠AOP=∠BOP,PD⊥OB,PE⊥OA,
∴PE=PD(角平分线上的点到角两边的距离相等),
∵∠BOP=∠AOP=15°,
∴∠AOB=30°,
∵PC∥OB,
∴∠ACP=∠AOB=30°,
∴在Rt△PCE中,PE=
| 1 |
| 2 |
| 1 |
| 2 |
∴PD=PE=1,
故选D.
点评:此题主要考查角平分线的性质和平行线的性质,难度一般,作辅助线是关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目
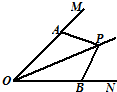 13、如图,点P在∠MON的平分线上,点A、B分别在角的两边,如果要使△AOP≌△BOP,那么需要添加的一个条件是
13、如图,点P在∠MON的平分线上,点A、B分别在角的两边,如果要使△AOP≌△BOP,那么需要添加的一个条件是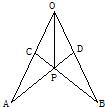 21、如图所示,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则下列结论正确的是( )
21、如图所示,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则下列结论正确的是( )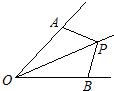 8、如图,已知∠AOP=∠BOP,若使△AOP≌△BOP,则下列需添加的一个条件不正确的是( )
8、如图,已知∠AOP=∠BOP,若使△AOP≌△BOP,则下列需添加的一个条件不正确的是( )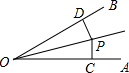 如图,P在∠AOB的内部,PC⊥AO于C,PD⊥OB于D,PD=PC,当∠AOP=x度,∠BOP=(110-4x)度时,∠AOP=
如图,P在∠AOB的内部,PC⊥AO于C,PD⊥OB于D,PD=PC,当∠AOP=x度,∠BOP=(110-4x)度时,∠AOP=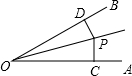 如图,P在∠AOB的内部,PC⊥AO于C,PD⊥OB于D,PD=PC,当∠AOP=(2x-10)度,∠BOP=(x+5)度时,∠AOB=
如图,P在∠AOB的内部,PC⊥AO于C,PD⊥OB于D,PD=PC,当∠AOP=(2x-10)度,∠BOP=(x+5)度时,∠AOB=