题目内容
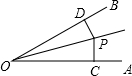 如图,P在∠AOB的内部,PC⊥AO于C,PD⊥OB于D,PD=PC,当∠AOP=(2x-10)度,∠BOP=(x+5)度时,∠AOB=
如图,P在∠AOB的内部,PC⊥AO于C,PD⊥OB于D,PD=PC,当∠AOP=(2x-10)度,∠BOP=(x+5)度时,∠AOB=40
40
度.分析:根据到角的两边距离相等的点在角的平分线上可得∠AOP=∠BOP,然后列出方程求出x,从而得到∠AOP、∠BOP,再根据∠AOB=∠AOP+∠BOP计算即可得解.
解答:解:∵PC⊥AO于C,PD⊥OB于D,PD=PC,
∴∠AOP=∠BOP,
∴2x-10=x+5,
解得x=15°,
∴∠AOP=∠BOP=15°+5°=20°,
∴∠AOB=∠AOP+∠BOP=20°+20°=40°.
故答案为:40.
∴∠AOP=∠BOP,
∴2x-10=x+5,
解得x=15°,
∴∠AOP=∠BOP=15°+5°=20°,
∴∠AOB=∠AOP+∠BOP=20°+20°=40°.
故答案为:40.
点评:本题考查了到角的两边距离相等的点在角的平分线上,熟记角平分线的判定方法是解题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
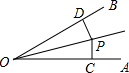 如图,P在∠AOB的内部,PC⊥AO于C,PD⊥OB于D,PD=PC,当∠AOP=x度,∠BOP=(110-4x)度时,∠AOP=
如图,P在∠AOB的内部,PC⊥AO于C,PD⊥OB于D,PD=PC,当∠AOP=x度,∠BOP=(110-4x)度时,∠AOP= 如图,P在∠AOB的平分线上,若PD=PE,须添加一个条件:
如图,P在∠AOB的平分线上,若PD=PE,须添加一个条件:
