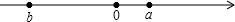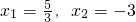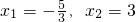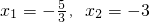题目内容
锐角△ABC的垂心关于三边的对称点分别是H1，H2，H3．已知：H1，H2，H3，求作△ABC．
作法：1、作△H1H2H3的外接圆O，2、连接H1H2，作H1H2的垂直平分线EF交圆O于A，同法可作H2H3和H1H3的垂直平分线，分别交圆于B、C，
3、连接AB、BC、AC，
则△ABC为所求．
分析：首先根据线段的垂直平分线的性质，推出垂心H关于三边的对称点，均在△ABC的外接圆上，作△H1H2H3的外接圆O，根据线段的垂直平分线的性质作出弧H1H2、弧H2H3、弧H1H3的中点即可得到答案．
点评：本题主要考查了三角形的五心，线段的垂直平分线的性质等知识点，解此题的关键是理解△ABC的垂心H关于三边的对称点，均在△ABC的外接圆上．题型较好，但有一定的难度．
练习册系列答案
阅读快车系列答案
相关题目
如图是某广场用地板铺设的部分图案，中央是一块正六边形的地板砖，周围是正三角形和正方形的地板砖．从里向外的第1层包括6个正方形和6个正三角形，第2层包括6个正方形和18个正三角形，依此递推，第8层中含有正三角形个数是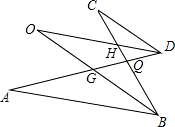
如图，已知DO平分∠ADC，BO平分∠ABC，且∠A=23°，∠O=25°，则∠C的大小是
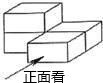由大小相同的长方体木块搭成的立体图形如图所示，则这个立体图形的正视图是
