题目内容
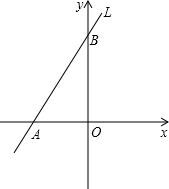如图所示，直线L与两坐标轴的交点坐标分别是A（-3，0），B（0，4），O是坐标系原点．（1）求直线L所对应的函数的表达式；
（2）若以AB为腰的等腰三角形交坐标轴于点C，求点C的坐标．
分析：（1）设出函数解析式，将两点代入，运用待定系数法求解；
（2）C点的位置比较多，每个坐标轴上有三个点，依次寻找即可．
（2）C点的位置比较多，每个坐标轴上有三个点，依次寻找即可．
解答：解：（1）设函数解析式为y=kx+b，
两点代入得：
，
解得：k=
，b=4，
∴函数解析式为：y=
x+4；
（2）AB为腰的等腰三角形交坐标轴与C点，C点可以有6个值，
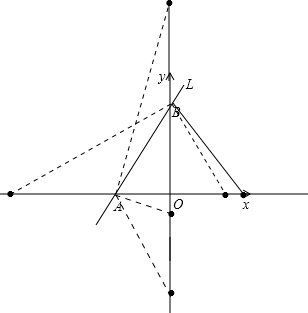
C点坐标分别为（3，0）（-8，0）（0，9）（0，-1）（0，-4）（2，0）．
两点代入得：
|
解得：k=
| 4 |
| 3 |
∴函数解析式为：y=
| 4 |
| 3 |
（2）AB为腰的等腰三角形交坐标轴与C点，C点可以有6个值，
C点坐标分别为（3，0）（-8，0）（0，9）（0，-1）（0，-4）（2，0）．
点评：本题考查待定系数法求函数解析式及关于y轴对称的点的坐标的特点，难度不大，注意掌握待定系数法的运用．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
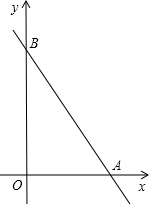如图所示，直线AB与两坐标轴的交点坐标分别是A（6，0），B（0，8），O是坐标系原点．
