题目内容
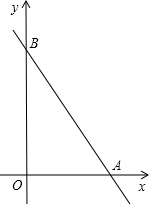 如图所示,直线AB与两坐标轴的交点坐标分别是A(6,0),B(0,8),O是坐标系原点.
如图所示,直线AB与两坐标轴的交点坐标分别是A(6,0),B(0,8),O是坐标系原点.(1)求直线AB所对应的函数的表达式;
(2)用尺规作图,作以O为圆心且与直线AB相切的⊙O;并求出⊙O的半径.
分析:(1)设直线的解析式是y=kx+b,根据直线经过A,B两个点用待定系数法求解;
(2)根据圆心到直线的距离等于圆的半径,则直线和圆相切,只需作出OD⊥AB于D,则OD即为圆的半径.根据直角三角形的面积可知:该高等于两条直角边的乘积除以斜边.
(2)根据圆心到直线的距离等于圆的半径,则直线和圆相切,只需作出OD⊥AB于D,则OD即为圆的半径.根据直角三角形的面积可知:该高等于两条直角边的乘积除以斜边.
解答: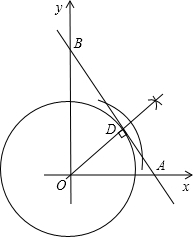 解:(1)设直线AB的函数解析式为y=kx+b.
解:(1)设直线AB的函数解析式为y=kx+b.
由已知可得:
;
解得:
.
所以直线AB的函数解析式是:y=-
x+8.
(2)如图:⊙O即为所求;
因为D是⊙O与直线AB的切点,则OD为⊙O的半径;
在Rt△AOB中,OA=6,OB=8所以AB=
=
=10,
因为
AB•OD=
OA•OB,
所以OD=
=
=
,
⊙O的半径为
.
 解:(1)设直线AB的函数解析式为y=kx+b.
解:(1)设直线AB的函数解析式为y=kx+b.由已知可得:
|
解得:
|
所以直线AB的函数解析式是:y=-
| 4 |
| 3 |
(2)如图:⊙O即为所求;
因为D是⊙O与直线AB的切点,则OD为⊙O的半径;
在Rt△AOB中,OA=6,OB=8所以AB=
| OA2+OB2 |
| 62+82 |
因为
| 1 |
| 2 |
| 1 |
| 2 |
所以OD=
| OA•OB |
| AB |
| 6×8 |
| 10 |
| 24 |
| 5 |
⊙O的半径为
| 24 |
| 5 |
点评:能够熟练运用待定系数法求得函数的解析式,根据直线和圆相切应满足的数量关系来确定圆的半径.

练习册系列答案
相关题目
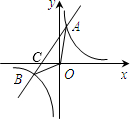 如图所示,直线AB与反比例函数
如图所示,直线AB与反比例函数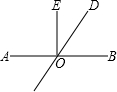 如图所示,直线AB与直线CD相交于点O,EO⊥AB,∠EOD=25°,则∠BOD=
如图所示,直线AB与直线CD相交于点O,EO⊥AB,∠EOD=25°,则∠BOD=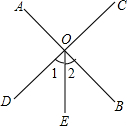 如图所示,直线AB与CD相交于O点,∠1=∠2.若∠AOE=140°,则∠AOC 的度数为( )
如图所示,直线AB与CD相交于O点,∠1=∠2.若∠AOE=140°,则∠AOC 的度数为( )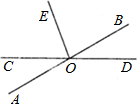 如图所示,直线AB与CD交于点O,∠BOD=31°36′,OE平分∠BOC,则∠AOD+∠COE=
如图所示,直线AB与CD交于点O,∠BOD=31°36′,OE平分∠BOC,则∠AOD+∠COE=