题目内容
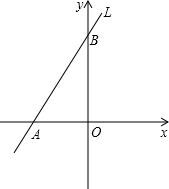
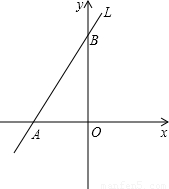
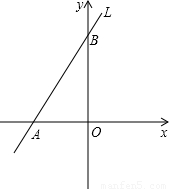
如图所示,直线L与两坐标轴的交点坐标分别是A(-3,0),B(0,4),O是坐标系原点.(1)求直线L所对应的函数的表达式;
(2)若以O为圆心,半径为R的圆与直线L相切,求R的值.
【答案】分析:(1)可把A,B两点的坐标代入,解方程组即可.
(2)相切那么O到L的距离等于半径,那么求出O到AB的距离即可.
解答: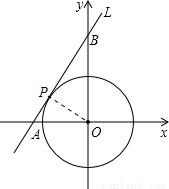 解:(1)设所求为y=kx+b.(1分)
解:(1)设所求为y=kx+b.(1分)
将A(-3,0),B(0,4)的坐标代入,得
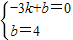 (2分)
(2分)
解得b=4,k= .(3分)
.(3分)
所求为y= x+4.(4分)
x+4.(4分)
(2)设切点为P,连OP,则OP⊥AB,OP=R.(5分)
Rt△AOB中,OA=3,OB=4,得AB=5,(6分)
因为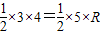 ,(7分)
,(7分)
∴R=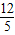 .(8分)
.(8分)
点评:一次函数的解析式为y=kx+b.本题需注意的知识点为:直线与圆相切,圆心到直线的距离等于半径.
(2)相切那么O到L的距离等于半径,那么求出O到AB的距离即可.
解答:
 解:(1)设所求为y=kx+b.(1分)
解:(1)设所求为y=kx+b.(1分)将A(-3,0),B(0,4)的坐标代入,得
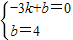 (2分)
(2分)解得b=4,k=
 .(3分)
.(3分)所求为y=
 x+4.(4分)
x+4.(4分)(2)设切点为P,连OP,则OP⊥AB,OP=R.(5分)
Rt△AOB中,OA=3,OB=4,得AB=5,(6分)
因为
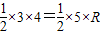 ,(7分)
,(7分)∴R=
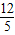 .(8分)
.(8分)点评:一次函数的解析式为y=kx+b.本题需注意的知识点为:直线与圆相切,圆心到直线的距离等于半径.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
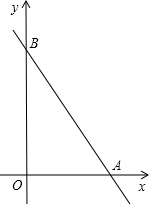 如图所示,直线AB与两坐标轴的交点坐标分别是A(6,0),B(0,8),O是坐标系原点.
如图所示,直线AB与两坐标轴的交点坐标分别是A(6,0),B(0,8),O是坐标系原点.