Question

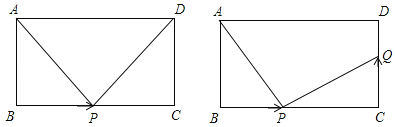
【题目】如图1，在△ABC中，∠BAC=90°，AB=AC，M、N是过点A的一条直线，作 BD⊥MN于点D，CE⊥MN于点E。

（1）求证：DE=BD+CE；

（2）当直线MN绕点A旋转到图2所示的位置，其他条件不变，则BD与DE、CE的关系如何？请予以证明

Answer 1

【答案】（1）证明见解析（2）BD=DE+CE

【解析】试题分析：（1）由题中条件可得Rt△ABD≌Rt△CAE，再由线段之间的关系写出最终结论即可；
（2）由HL得出Rt△ABD≌Rt△CAE，进而得出BD=AE，AD=CE，再由线段之间的转化即可得出结论：BD=DE+CE或DE=BD-CE．

试题解析：

（1）∵BD⊥直线MN，CE⊥直线MN，

∴∠BDA=∠AEC=90°，

∵∠BAC=90°，

∴∠BAD+∠CAE=90°，

∵∠BAD+∠ABD=90°，

∴∠CAE=∠ABD，

∵在△ADB和△CEA中

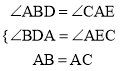
∴△ADB≌△CEA

∴AE=BD，AD=CE，

∴DE=AE+AD=BD+CE；

（2）关系：BD=DE+CE

证明如下：

∵BD⊥直线MN，CE⊥直线MN，

∴∠BDA=∠AEC=90°，

∵∠BAC=90°，

∴∠BAD+∠CAE=90°，

∵∠BAD+∠ABD=90°，

∴∠CAE=∠ABD，

∵在△ADB和△CEA中

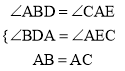
∴△ADB≌△CEA

∴AE=BD，AD=CE，

∴BD=AE=DE+AD=DE+CE.