题目内容

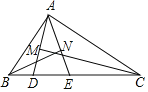
【题目】如图，已知矩形，点在边上，连接将沿翻折，得到，且点是中点，取中点，点为线段上一动点，连接，，若长为2，则的最小值为__________.

【答案】2

【解析】

作点N关于BE的对称点N'，连接PN'，由轴对称的性质可得PN+PM=PN'+PM，依据当N'，P，M三点共线时，PM+PN的最小值为N'M的长，即可得到PM+PN的最小值为2．

如图，作点N关于BE的对称点N'，连接PN'，


由折叠可得，BE平分∠ABM，AB=MB，
∴点N'在AB上，
又∵N是BM的中点，
∴N'是AB的中点，
由轴对称的性质可得PN=PN'，
∴PN+PM=PN'+PM，
∴当N'，P，M三点共线时，PM+PN的最小值为N'M的长，
又∵四边形ABCD是矩形，M是CD的中点，
∴四边形ADMN'是矩形，
∴MN'=AD=2，
∴PM+PN的最小值为2，
故答案为：2．

练习册系列答案
相关题目

【题目】如图，下列条件不能判定四边形ABCD是矩形的是（　　）

A.∠DAB＝∠ABC＝∠BCD＝90°B.AB∥CD，AB＝CD，AB⊥AD

C.AO＝BO，CO＝DOD.AO＝BO＝CO＝DO

【题目】如图，△ABC的周长为17，点D，E在边BC上，∠ABC的平分线垂直于AE，垂足为点N，∠ACB的平分线垂直于AD，垂足为点M，若BC＝6，则MN的长度为_____．

【题目】如图，抛物线y=ax2+bx(a≠0) 交x轴正半轴于点A，直线y=2x 经过抛物线的顶点M．已知该抛物线的对称轴为直线x=2，交x轴于点B．

（1）求a，b的值；

（2）P是第一象限内抛物线上的一点，且在对称轴的右侧，连接OP，BP．设点P的横坐标为m ，△OBP的面积为S，．求K关于m 的函数表达式及K的范围．

【题目】阅读下面的情景对话，然后解答问题：

老师：我们定义一种三角形，两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.

小华：等边三角形一定是奇异三角形！

小明：那直角三角形中是否存在奇异三角形呢？

问题（1）：根据“奇异三角形”的定义，请你判断小华提出的猜想：“等边三角形一定是奇异三角形”是否正确？___________填“是”或“否”）

问题（2）：已知中，两边长分别是5，，若这个三角形是奇异三角形，则第三边长是_____________；

问题（3）：如图，以为斜边分别在的两侧作直角三角形，且，若四边形内存在点，使得，.试说明：是奇异三角形.

【题目】如图是抛物线形拱桥，当拱顶离水面2m时，水面宽4m，则水面下降1m时，水面宽度增加_____m．

【题目】如图，下列条件不能判定四边形ABCD是矩形的是（　　）

A.∠DAB＝∠ABC＝∠BCD＝90°B.AB∥CD，AB＝CD，AB⊥AD

C.AO＝BO，CO＝DOD.AO＝BO＝CO＝DO

【题目】已知正方形ABCD与正方形CEFG，M是AF的中点，连接DM，EM．

（1）如图1，点E在CD上，点G在BC的延长线上，请判断DM，EM的数量关系与位置关系，并直接写出结论；

（2）如图2，点E在DC的延长线上，点G在BC上，（1）中结论是否仍然成立？请证明你的结论；

（3）将图1中的正方形CEFG绕点C旋转，使D，E，F三点在一条直线上，若AB=13，CE=5，请画出图形，并直接写出MF的长．

【题目】某中学采用随机的方式对学生掌握安全知识的情况进行测评，并按成绩高低分成优、良、中、差四个等级进行统计，绘制了下面两幅尚不完整的统计图．请根据有关信息解答：

(1)接受测评的学生共有________人，扇形统计图中“优”部分所对应扇形的圆心角为________°，并补全条形统计图；

(2)若该校共有学生1200人，请估计该校对安全知识达到“良”程度的人数；

(3)测评成绩前五名的学生恰好3个女生和2个男生，现从中随机抽取2人参加市安全知识竞赛，请用树状图或列表法求出抽到1个男生和1个女生的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网