Question

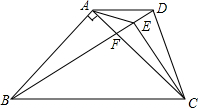如图，梯形ABCD中，AD∥BC，AB=AC，AB⊥AC，BC=BD，E为FD中点，下列结论中：
①∠ADB=30°；②AD=

1

2

BC；③AD=

2

AE；④EB-EC=

2

EA．其中正确的结论是（　　）

A．①②③

B．①④

C．①③④

D．①③

Answer 1

分析：过A作AM⊥BC于M，过D作DN⊥BC于N，求出AM=DN=

1

2

BC=

1

2

BD，推出∠DBC=30°，即可判断①；求出AM=

1

2

BC，即可判断②；作AQ⊥AE交BD于Q，证△ABQ≌△ACE，推出BQ=CE，AQ=AE，即可判断④；过A作AR⊥DQ于R，求出AD=QE=，即可判断③．

解答：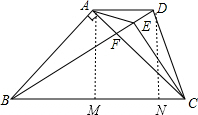
解：如图，过A作AM⊥BC于M，过D作DN⊥BC于N，
则AM∥DN，
∵AD∥BC，
∴AM=DN，
∵AB=AC，AB⊥AC，AM⊥BC，
∴∠BAC=90°，
∴AM=

1

2

BC，∠ABC=∠ACB=45°，
∴AB=AC，DN=

1

2

BC，
∵BC=BD，
∴DN=

1

2

BD，
∵∠BAC=90°，
∴∠DBC=30°，
∵AD∥BC，
∴∠ADB=∠DBC=30°，∴①正确；
∵∠BAC=90°，AB=AC，AM⊥BC，
∴AM=

1

2

BC，根据已知不能推出AD=AM，∴②错误；

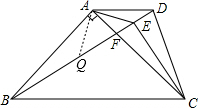
作AQ⊥AE交BD于Q，过A作AR⊥DQ于R，
∵∠ADB=30°，
∴2AR=AD，
则∠QAE=∠BAC=90°，
∴∠QAE-∠QAF=∠BAC-∠QAE，
∴∠BAQ=∠CAE，
∵∠ABC=45°，∠DBC=30°，
∴∠ABQ=15°，
∵BD=BC，∠DBC=30°，
∴∠BDC=∠BCD=75°，
∵∠ACB=45°，
∴∠DCF=30°，
∵∠AF=15°，∠BAC=90°，
∴∠AFB=75°=∠DFC=∠CDB，
∴CF=CD，
∵E为DF中点，
∴∠ECA=

1

2

∠DCF=15°=∠ABQ，
∵在△ABQ和△ACE中

∠ABQ=∠ACE AB=AC ∠BAQ=∠CAE

，
∴△ABQ≌△ACE（ASA），
∴AQ=AE，BQ=CE，
∴在Rt△QAE中，AQ=AE，由勾股定理得：QE=

2

AE，
即EB-EC=

2

AE，∴④正确；
过A作AR⊥DQ于R，
∵∠ADB=30°，
∴2AR=AD，
∵∠QAE=90°，AQ=AE，AR⊥QE，
∴2AR=QE，
∴AD=QE，
在Rt△QAE中，由勾股定理得：QE=

2

AE，
即AD=

2

AE，∴③正确．
故选C．

点评：本题考查了全等三角形的性质和判定，勾股定理，平行线的性质，含30度角的直角三角形性质，等腰三角形的性质和判定等知识点的综合运用，综合性比较强，难度偏大．