题目内容
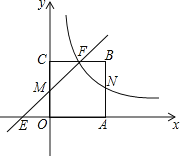
【题目】如图,点A是⊙O上一点,OA⊥AB,且OA=1,AB=![]() ,OB交⊙O于点D,作AC⊥OB,垂足为M,并交⊙O于点C,连接BC.
,OB交⊙O于点D,作AC⊥OB,垂足为M,并交⊙O于点C,连接BC.
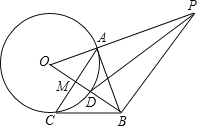
(1)求证:BC是⊙O的切线;
(2)过点B作BP⊥OB,交OA的延长线于点P,连接PD,求sin∠BPD的值.
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)连结OC,根据垂径定理由AC⊥OB得AM=CM,于是可判断OB为线段AC的垂直平分线,所以BA=BC,然后利用“SSS”证明△OAB≌△OCB,得到∠OAB=∠OCB,由于∠OAB=90°,则∠OCB=90°,于是可根据切线的判定定理得BC是⊙O的切线;
(2)在Rt△OAB中,根据勾股定理计算出OB=2,根据含30度的直角三角形三边的关系得∠ABO=30°,∠AOB=60°,在Rt△PBO中,由∠BPO=30°得到PB=![]() OB=2
OB=2![]() ;在Rt△PBD中,BD=OB﹣OD=1,根据勾股定理计算出PD=
;在Rt△PBD中,BD=OB﹣OD=1,根据勾股定理计算出PD=![]() ,然后利用正弦的定义求sin∠BPD的值.
,然后利用正弦的定义求sin∠BPD的值.
(1)证明:连结OC,如图,
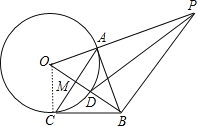
∵AC⊥OB,
∴AM=CM,
∴OB为线段AC的垂直平分线,
∴BA=BC,
在△OAB和△OCB中
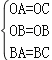 ,
,
∴△OAB≌△OCB(SSS),
∴∠OAB=∠OCB,
∵OA⊥AB,
∴∠OAB=90°,
∴∠OCB=90°,
∴OC⊥BC,
故BC是⊙O的切线;
(2)解:在Rt△OAB中,OA=1,AB=![]() ,
,
∴OB=![]() =2,
=2,
∴∠ABO=30°,∠AOB=60°,
∵PB⊥OB,
∴∠PBO=90°,∠BPO=30°,
在Rt△PBO中,OB=2,
∴PB=![]() OB=2
OB=2![]() ,
,
在Rt△PBD中,BD=OB﹣OD=2﹣1=1,PB=2![]() ,
,
∴PD=![]() =
=![]() ,
,
∴sin∠BPD=![]() =
=![]() =
=![]() .
.

练习册系列答案
相关题目