题目内容
【题目】两块完全相同的三角板Ⅰ(△ABC)和Ⅱ(△A1B1C1)如图①放置在同一平面上(∠C=∠C1=90°,∠ABC=∠A1B1C1=60°),斜边重合.若三角板Ⅱ不动,三角板Ⅰ在三角板Ⅱ所在的平面上向右滑动,图②是滑动过程中的一个位置.
(1)在图②中,连接BC1、B1C,求证:△A1BC1≌△AB1C;
(2)三角板Ⅰ滑到什么位置(点B1落在AB边的什么位置)时,四边形BCB1C1是菱形?说明理由.
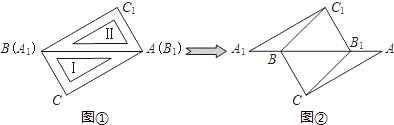
【答案】(1)证明见解析;(2)点B1落在AB边的中点.理由见解析.
【解析】
(1)根据三角板Ⅰ(△ABC)和Ⅱ(△A1B1C1)是两块完全相同的三角板可得AC=A1C1,AB=A1B1,∠A=∠A1,再根据公共边,即可得到结果.
(2)由已知条件可得四边形BCB1C1是平行四边形,再证明△BCB1为等边三角形,可得到BB1=B1C=BC,可得到结果.
(1)证明:∵三角板Ⅰ(△ABC)和Ⅱ(△A1B1C1)是两块完全相同的三角板,
∴AC=A1C1,AB=A1B1,∠A=∠A1
∴在图②中A1B=AB1
∴△A1BC1≌△AB1C.
(2)解:点B1落在AB边的中点.理由如下:
如图②所示,由已知条件知BC=B1C1,BC∥B1C1
∴四边形BCB1C1是平行四边形.
要使四边形BCB1C1是菱形,
则BC=CB1
∵∠ABC=∠A1B1C1=60°,
∴△BCB1为等边三角形.
∴BB1=B1C=BC,
又∵∠A=30°,
在直角三角形ABC中,BC=![]() AB,
AB,
∴BB1=![]() AB,
AB,
∴点B1落在AB边的中点.

练习册系列答案
相关题目