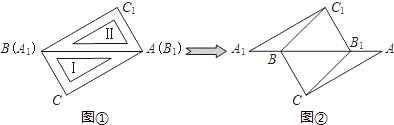��Ŀ����
����Ŀ����ͼ����һ�ų�10cm����8cm�ij�����Ӳֽ������ܸ���ȥһ��ͬ����С�������Σ����ۺϳ�һ���ǵij�������ӣ�ֽ��ĺ�Ⱥ��Բ��ƣ���
��1��Ҫʹ�dz�������ӵĵ����Ϊ48cm2����ô��ȥ�������εı߳�Ϊ���٣�
��2������ѳ�����Ӳֽ������ֱܷ��ȥ2��ͬ����С�������κ�2��ͬ����״��ͬ����С�ij����Σ�Ȼ���ۺϳ�һ���иǵij�������ӣ���ô���IJ������ָ���Ǹ�Ϊ��ȥ�������α߳��ij�����IJ���������Դﵽ30cm2����˵�����ɣ�

���𰸡���1����ȥ�������εı߳�Ϊ1cm����2����ȥ�������α߳�Ϊ![]() cm��3cm��
cm��3cm��
��������
��1�����ȥ�������α߳�Ϊxcm�����ݳ����ε������ʽ���з��̣�10-2x����8-2x��=48����������̣��Ѳ�������Ľ���ȥ�����ɵõ�����𰸣�
��2�����ȥ�������α߳�Ϊycm���������ּ���������ͼ1����ʱ��2(8-2y)y+2��![]() y=30����ñ�������ʵ���⣻����ͼ2����ʱ���з���2(10-2y)y+2��
y=30����ñ�������ʵ���⣻����ͼ2����ʱ���з���2(10-2y)y+2��![]() y=30����˷��̣����ɵñ�С��𰸣�
y=30����˷��̣����ɵñ�С��𰸣�
�⣺��1�����ȥ�������α߳�Ϊxcm�������⣬��
��10-2x����8-2x��=48����x2-9x+8=0
���x1=8���������⣬��ȥ����x2=1��
���ȥ�������εı߳�Ϊ1cm��
��2�����IJ�������Դﵽ30cm2���������£�
���ȥ�������α߳�Ϊycm��
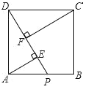
����ͼ1��ʾ�ķ������ۣ�
�ⷽ��2(8-2y)y+2��![]() y=30���ø÷���û��ʵ���⣮
y=30���ø÷���û��ʵ���⣮
����ͼ2��ʾ�ķ������ۣ�
�ⷽ��2(10-2y)y+2��![]() y=30��
y=30��
��y1=![]() ��y2=3��
��y2=3��
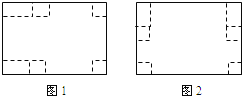
�൱��ͼ2��ʾ�ķ�����ȥ�������α߳�Ϊ![]() cm��3cmʱ����ʹ�õ����иdz�������ӵIJ�����ﵽ30 cm2��
cm��3cmʱ����ʹ�õ����иdz�������ӵIJ�����ﵽ30 cm2��