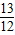题目内容
（2009•福州质检）如图，将矩形EFBC一条对角线FC向两端延伸，使AF=DC，连接AB、ED，求证：△AFB≌△DCE．
【答案】分析：本题中，已知了AF=DC，根据矩形的性质可得出BF=CE，那么只要证明∠AFB=∠DCE即可，那么根据BF∥CE，可得出∠BFC=∠FCE，进而推导出∠BFA=∠DCE，这样就符合了全等三角形判定中的边角边．
解答：证明：在△AFB和△DCE中，
由矩形EFBC可得：
BF=EC，BF∥EC，
∴∠BFC=∠FCE．
∴∠BFA=∠DCE．
又AF=DC，
∴△AFB≌△DCE（SAS）．
点评：三角形全等的判定是中考的热点，一般以考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．
解答：证明：在△AFB和△DCE中，
由矩形EFBC可得：
BF=EC，BF∥EC，
∴∠BFC=∠FCE．
∴∠BFA=∠DCE．
又AF=DC，
∴△AFB≌△DCE（SAS）．
点评：三角形全等的判定是中考的热点，一般以考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（x＞0，k＞0）的图象交于点A，以坐标原点O为圆心，OA长为半径画弧，交x轴正半轴于点C，直线AB交x轴负半轴于B点，∠ABC=30°．
的值；（其中，S为△AOB面积，T为扇形AOC面积）
-
+
-
+…-
+
的值．
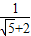），tan45°，（
+2），（
-2）四个数中任选三个组成一个算式，并计算结果；
-
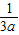，y=
-
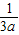，请计算x+y的结果．
