题目内容
(2009•福州质检)如图,三角形ADC是由等腰直角三角形EOG经过位似变换得到的,变换中心在x轴的正半轴,已知EO=1,D点坐标为D(2,0),位似比为1:2,则两个三角形的位似中心P点的坐标是 .
【答案】分析:先求G点的坐标分别为(0,-1),D点坐标为D(2,0),位似比为1:2,A点的坐标为(2,2),再求出直线AG的解析式为y= x-1,得到直线AG与x的交点坐标,即两个三角形的位似中心P点的坐标.
x-1,得到直线AG与x的交点坐标,即两个三角形的位似中心P点的坐标.
解答:解:∵△ADC与△EOG都是等腰直角三角形
∴OE=OG
∴G点的坐标分别为(0,-1)
∵D点坐标为D(2,0),位似比为1:2,
∴A点的坐标为(2,2)
∴直线AG的解析式为y= x-1
x-1
∴直线AG与x的交点坐标为( ,0)
,0)
∴两个三角形的位似中心P点的坐标是( ,0).
,0).
点评:本题考查了位似的相关知识,位似图形的对应顶点的连线过同一点,此点为位似中心.
 x-1,得到直线AG与x的交点坐标,即两个三角形的位似中心P点的坐标.
x-1,得到直线AG与x的交点坐标,即两个三角形的位似中心P点的坐标.解答:解:∵△ADC与△EOG都是等腰直角三角形
∴OE=OG
∴G点的坐标分别为(0,-1)
∵D点坐标为D(2,0),位似比为1:2,
∴A点的坐标为(2,2)
∴直线AG的解析式为y=
 x-1
x-1∴直线AG与x的交点坐标为(
 ,0)
,0)∴两个三角形的位似中心P点的坐标是(
 ,0).
,0).点评:本题考查了位似的相关知识,位似图形的对应顶点的连线过同一点,此点为位似中心.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 (x>0,k>0)的图象交于点A,以坐标原点O为圆心,OA长为半径画弧,交x轴正半轴于点C,直线AB交x轴负半轴于B点,∠ABC=30°.
(x>0,k>0)的图象交于点A,以坐标原点O为圆心,OA长为半径画弧,交x轴正半轴于点C,直线AB交x轴负半轴于B点,∠ABC=30°. 的值;(其中,S为△AOB面积,T为扇形AOC面积)
的值;(其中,S为△AOB面积,T为扇形AOC面积) -
- +
+ -
- +…-
+…- +
+ 的值.
的值.
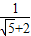 ),tan45°,(
),tan45°,( +2),(
+2),( -2)四个数中任选三个组成一个算式,并计算结果;
-2)四个数中任选三个组成一个算式,并计算结果; -
-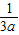 ,y=
,y=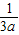 -
- ,请计算x+y的结果.
,请计算x+y的结果.