题目内容
(2009•福州质检)已知直线y=x与函数y= (x>0,k>0)的图象交于点A,以坐标原点O为圆心,OA长为半径画弧,交x轴正半轴于点C,直线AB交x轴负半轴于B点,∠ABC=30°.
(x>0,k>0)的图象交于点A,以坐标原点O为圆心,OA长为半径画弧,交x轴正半轴于点C,直线AB交x轴负半轴于B点,∠ABC=30°.(1)画出满足题意的示意图;
(2)请用含π的代数式表示
 的值;(其中,S为△AOB面积,T为扇形AOC面积)
的值;(其中,S为△AOB面积,T为扇形AOC面积)(3)设k取k1时,△AOB面积为S1,扇形AOC面积为T1,k取k2时,△AOB面积为S2,扇形AOC面积为T2…求
 -
- +
+ -
- +…-
+…- +
+ 的值.
的值.
【答案】分析:(1)首先确定点C的位置,再进一步画出30度的角确定点B的位置;
(2)首先根据直线和双曲线的解析式可以求得交点A的坐标,作AD⊥x轴于D,则得到等腰直角三角形AOD.根据勾股定理求得OA的长,即可表示出扇形的面积;要求OB的长,根据30度的直角三角形的性质求得BD的长,从而求得OB的长,即可表示出三角形的面积.最后求得比值;
(3)根据(2)的结论,不难看到它们之间的面积比是一个定值,利用抵消的方法即可求解.
解答:解:(1)画图正确(3分)

(2)由题意可得A点坐标为(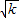 ,
,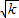 )过A作AD⊥x轴于D,(1分)
)过A作AD⊥x轴于D,(1分)
BO=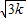 -
-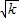 ,AD=
,AD=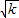 ,OA=
,OA=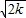 (1分)
(1分)
∴△AOB的面积S=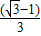 k(1分)
k(1分)
扇形AOC面积T= k(1分)
k(1分)
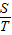 =
=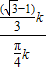 =
=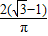
因此无论k值如何变化,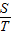 的值都不变,
的值都不变,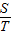 =
=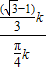 =
=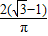 ;(3分)
;(3分)
(3)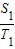 -
-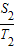 +
+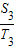 -
-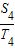 +-
+-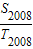 +
+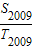 =
=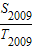 =
=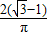 .
.
点评:注意:直线y=x即是第一、三象限的角平分线,可以出现等腰直角三角形.掌握等腰直角三角形和30度的直角三角形的性质,熟悉三角形和扇形的面积公式.
(2)首先根据直线和双曲线的解析式可以求得交点A的坐标,作AD⊥x轴于D,则得到等腰直角三角形AOD.根据勾股定理求得OA的长,即可表示出扇形的面积;要求OB的长,根据30度的直角三角形的性质求得BD的长,从而求得OB的长,即可表示出三角形的面积.最后求得比值;
(3)根据(2)的结论,不难看到它们之间的面积比是一个定值,利用抵消的方法即可求解.
解答:解:(1)画图正确(3分)

(2)由题意可得A点坐标为(
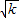 ,
,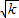 )过A作AD⊥x轴于D,(1分)
)过A作AD⊥x轴于D,(1分)BO=
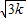 -
-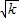 ,AD=
,AD=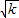 ,OA=
,OA=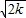 (1分)
(1分)∴△AOB的面积S=
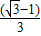 k(1分)
k(1分)扇形AOC面积T=
 k(1分)
k(1分)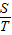 =
=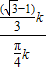 =
=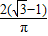
因此无论k值如何变化,
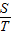 的值都不变,
的值都不变,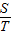 =
=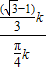 =
=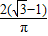 ;(3分)
;(3分)(3)
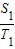 -
-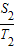 +
+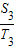 -
-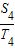 +-
+-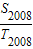 +
+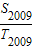 =
=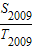 =
=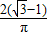 .
.点评:注意:直线y=x即是第一、三象限的角平分线,可以出现等腰直角三角形.掌握等腰直角三角形和30度的直角三角形的性质,熟悉三角形和扇形的面积公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


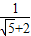 ),tan45°,(
),tan45°,( +2),(
+2),( -2)四个数中任选三个组成一个算式,并计算结果;
-2)四个数中任选三个组成一个算式,并计算结果; -
-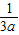 ,y=
,y=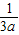 -
- ,请计算x+y的结果.
,请计算x+y的结果.