题目内容
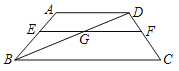
【题目】(已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.
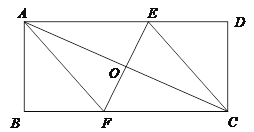
(1)求证:四边形AFCE是菱形;
(2)若AE=10cm,△ABF的面积为24cm2,求△ABF的周长;
(3)在线段AC上是否存在一点P,使得2AE2=AC·AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.
【答案】(1)证明见解析;(2)24cm;(3)存在,过E作EP⊥AD交AC于P,则P就是所求的点,证明见解析.
【解析】
(1)由四边形ABCD是矩形与折叠的性质,易证得△AOE≌△COF,即可得AE=CF,则可证得四边形AFCE是平行四边形,又由AC⊥EF,则可证得四边形AFCE是菱形;
(2)由已知可得:S△ABF=![]() ABBF=24cm2,则可得AB2+BF2=(AB+BF)2-2ABBF=(AB+BF)2-2×48=AF2=100(cm2),则可求得AB+BF的值,继而求得△ABF的周长.
ABBF=24cm2,则可得AB2+BF2=(AB+BF)2-2ABBF=(AB+BF)2-2×48=AF2=100(cm2),则可求得AB+BF的值,继而求得△ABF的周长.
(3)过E作EP⊥AD交AC于P,则P就是所求的点,首先证明四边形AFCE是菱形,然后根据题干条件证明△AOE∽△AEP,列出关系式.
解:(1)∵四边形ABCD是矩形,
∴AD∥BC,∴∠EAO=∠FCO,
由折叠的性质可得:OA=OC,AC⊥EF,
在△AOE和△COF中,
∵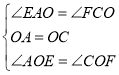 ,
,
∴△AOE≌△COF(ASA),
∴AE=CF,
∴四边形AFCE是平行四边形,
∵AC⊥EF,
∴四边形AFCE是菱形;
(2)∵四边形AFCE是菱形,
∴AF=AE=10cm,
∵四边形ABCD是矩形,
∴∠B=90°,
∴S△ABF=![]() ABBF=24cm2,
ABBF=24cm2,
∴ABBF=48(cm2),
∴AB2+BF2=(AB+BF)2-2ABBF=(AB+BF)2-2×48=AF2=100(cm2),
∴AB+BF=14(cm)
∴△ABF的周长为:AB+BF+AF=14+10=24(cm).
(3)证明:过E作EP⊥AD交AC于P,则P就是所求的点.
当顶点A与C重合时,折痕EF垂直平分AC,
∴OA=OC,∠AOE=∠COF=90°,
∵在平行四边形ABCD中,AD∥BC,
∴∠EAO=∠FCO,
∴△AOE≌△COF,
∴OE=OF
∴四边形AFCE是菱形.
∴∠AOE=90°,又∠EAO=∠EAP,
由作法得∠AEP=90°,
∴△AOE∽△AEP,
∴![]() ,则AE2=AOAP,
,则AE2=AOAP,
∵四边形AFCE是菱形,
∴AO=![]() AC,
AC,
∴AE2=![]() ACAP,
ACAP,
∴2AE2=ACAP.

 导学教程高中新课标系列答案
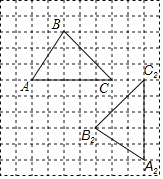
导学教程高中新课标系列答案【题目】如图,∠MAN=30°,在射线AN上取一点B,使AB=4 cm,过点B作BC⊥AM于点C,点D为边AB上的动点(点D不与点A,点B重合),连接CD,过点D作ED⊥CD交直线AC于点E.在点D由点A到点B运动过程中,设AD=x cm,AE=y cm.
(1)取指定点作图,根据下面表格预填结果,先通过作图确定AD=2 cm时,点E的位置,测量AE的长度.
①根据题意,在答题卡上补全图形;
②把表格补充完整:通过取点、画图、测量,得到了x与y的几组对应值,如表:
x/cm | … |
| 1 |
| 2 |
| 3 |
| … |
y cm | … | 0.4 | 0.8 | 1.0 | m | 1.0 | 0 | 4.0 | … |
则m=______(结果保留一位小数).
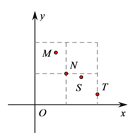
(2)在下面的平面直角坐标系xOy中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当AE=![]() AD时,AD的长度约为______cm.
AD时,AD的长度约为______cm.