题目内容
在工程爆破时,已知导火索燃烧的速度为0.5cm/s,人跑开时速度是4 cm/s,为了使放炮的人在爆破前能跑到100m以外的安全区域,导火索的长度x(cm)应满足的不等式是
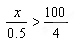
本题考察不等式的相关知识,列不等式方程,解不等式方程,和不等式的性质等知识。培养分析问题及解决问题的能力,会将实际问题转化成数学问题的能力。
解题思路:列不等式和等式一样,要找到核心关系,此题可以时间或者距离为核心列式。距离应该大于100m;时间应该是导火索燃尽时间大于人跑离的时间。
具体解题过程:设导火索长度为x(cm),则导火索燃尽的时间为x/0.5(s),而人跑出的距离为:x/0.5(s)X4cm/s=8x(cm)。而人跑离的距离应该大于100m=10000cm.因此,不等式应该是:
8x>10000
若以时间列式,则应该为:
X/0.5>10000/4
本题小结:由于是七年级的学生练习题,所以应该注重基础知识的理解与应用。结合学生以往的知识积累,逐步培养分析解决问题的能力为主攻方向,简单的题目,要详细讲解解决。
解题思路:列不等式和等式一样,要找到核心关系,此题可以时间或者距离为核心列式。距离应该大于100m;时间应该是导火索燃尽时间大于人跑离的时间。
具体解题过程:设导火索长度为x(cm),则导火索燃尽的时间为x/0.5(s),而人跑出的距离为:x/0.5(s)X4cm/s=8x(cm)。而人跑离的距离应该大于100m=10000cm.因此,不等式应该是:
8x>10000
若以时间列式,则应该为:
X/0.5>10000/4
本题小结:由于是七年级的学生练习题,所以应该注重基础知识的理解与应用。结合学生以往的知识积累,逐步培养分析解决问题的能力为主攻方向,简单的题目,要详细讲解解决。

练习册系列答案
相关题目
 (℃)的变化范围是( )
(℃)的变化范围是( )  的解集是0≤x<1,求a、b的值
的解集是0≤x<1,求a、b的值 的整数解是____ 。
的整数解是____ 。 的过程中错误的是( )
的过程中错误的是( )



 的正整数解是方程
的正整数解是方程 的解,求
的解,求 的值。(8分)
的值。(8分)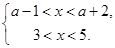 的解集是3<x<a+2,则a的取值范围是( )
的解集是3<x<a+2,则a的取值范围是( ) ,当
,当 满足 时,有
满足 时,有
 ≤
≤ .
.