题目内容
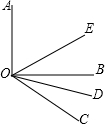 如图所示,OE,OD分别平分∠AOC和∠BOC.
如图所示,OE,OD分别平分∠AOC和∠BOC.(1)如果∠AOB=90°,∠BOC=40°,求∠DOE的度数;
(2)如果∠AOB=α,∠BOC=β(α、β均为锐角,α>β),其他条件不变,求∠DOE;
(3)从(1)、(2)的结果中,你发现了什么规律.
分析:(1)根据角平分线的定义,求得∠COE和∠COD的度数,结合图形,知∠DOE=∠COE-∠COD;
(2)和(1)的计算方法一样;
(3)综合(1)和(2)的结论,发现规律:∠DOE=
∠AOB.
(2)和(1)的计算方法一样;
(3)综合(1)和(2)的结论,发现规律:∠DOE=
| 1 |
| 2 |
解答:解:(1)∵∠AOB=90°,∠BOC=40°
∴∠AOC=∠AOB+∠BOC=90°+40°=130°.
又∵OE,OD分别平分∠AOC和∠BOC,
∴∠COE=
∠AOC=
×130°=65°,
∠COD=
∠BOC=
×40°=20°.
∴∠DOE=∠COE-∠COD=65°-20°=45°;
(2)∵∠AOB=α,∠BOC=β
∴∠AOC=∠AOB+∠BOC=α+β.
又∵OE,OD分别平分∠AOC和∠BOC,
∴∠COE=
∠AOC=
(α+β),
∠COD=
∠BOC=
β.
∴∠DOE=∠COE-∠COD=
(α+β)-
β
=
α+
β-
β
=
α;
(3)∠DOE的大小与∠BOC的大小无关,即∠DOE=
∠AOB.
∴∠AOC=∠AOB+∠BOC=90°+40°=130°.
又∵OE,OD分别平分∠AOC和∠BOC,
∴∠COE=
| 1 |
| 2 |
| 1 |
| 2 |
∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DOE=∠COE-∠COD=65°-20°=45°;
(2)∵∠AOB=α,∠BOC=β
∴∠AOC=∠AOB+∠BOC=α+β.
又∵OE,OD分别平分∠AOC和∠BOC,
∴∠COE=
| 1 |
| 2 |
| 1 |
| 2 |
∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DOE=∠COE-∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
(3)∠DOE的大小与∠BOC的大小无关,即∠DOE=
| 1 |
| 2 |
点评:此题主要是考查了角平分线的定义和角的和、差计算方法.

练习册系列答案
相关题目
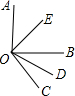 如图所示,OE,OD分别平分∠AOB和∠BOC,若∠AOB=90°,∠EOD=70°,求∠BOC的度数.
如图所示,OE,OD分别平分∠AOB和∠BOC,若∠AOB=90°,∠EOD=70°,求∠BOC的度数.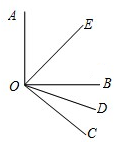 如图所示,OE,OD分别平分∠AOB和∠BOC,且∠AOB=90°;
如图所示,OE,OD分别平分∠AOB和∠BOC,且∠AOB=90°; 如图所示,OE,OD分别平分∠AOC和∠BOC,
如图所示,OE,OD分别平分∠AOC和∠BOC,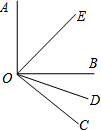 如图所示,OE和OD分别是∠AOB和∠BOC的平分线,且∠AOB=90°,∠BOC=40°,求∠EOD的度数.
如图所示,OE和OD分别是∠AOB和∠BOC的平分线,且∠AOB=90°,∠BOC=40°,求∠EOD的度数.