题目内容
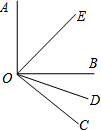 如图所示,OE和OD分别是∠AOB和∠BOC的平分线,且∠AOB=90°,∠BOC=40°,求∠EOD的度数.
如图所示,OE和OD分别是∠AOB和∠BOC的平分线,且∠AOB=90°,∠BOC=40°,求∠EOD的度数.分析:根据图示找出所求各角之间的关系,∠EOD=∠EOB+∠BOD,利用角平分线的性质,求出这个角的度数,即可求结果.
解答:解:根据题意:
∵OE,OD分别平分∠AOB和∠BOC,且∠AOB=90°,
∴∠EOB=
∠AOB=
×90°=45°
∠BOD=
∠BOC=
×40°=20°
所以:∠EOD=∠EOB+∠BOD=65°;
∵OE,OD分别平分∠AOB和∠BOC,且∠AOB=90°,
∴∠EOB=
| 1 |
| 2 |
| 1 |
| 2 |
∠BOD=
| 1 |
| 2 |
| 1 |
| 2 |
所以:∠EOD=∠EOB+∠BOD=65°;
点评:本题考查了角的计算及角平分线的定义,首先确定各角之间的关系,利用角平分线的性质来求.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
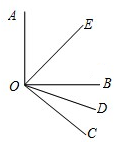 如图所示,OE,OD分别平分∠AOB和∠BOC,且∠AOB=90°;
如图所示,OE,OD分别平分∠AOB和∠BOC,且∠AOB=90°;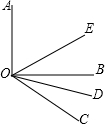 如图所示,OE,OD分别平分∠AOC和∠BOC.
如图所示,OE,OD分别平分∠AOC和∠BOC. 如图所示,OE,OD分别平分∠AOC和∠BOC,
如图所示,OE,OD分别平分∠AOC和∠BOC,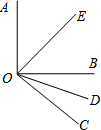 如图所示,OE和OD分别是∠AOB和∠BOC的平分线,且∠AOB=90°,∠BOC=40°,求∠EOD的度数.
如图所示,OE和OD分别是∠AOB和∠BOC的平分线,且∠AOB=90°,∠BOC=40°,求∠EOD的度数.