题目内容
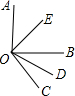 如图所示,OE,OD分别平分∠AOB和∠BOC,若∠AOB=90°,∠EOD=70°,求∠BOC的度数.
如图所示,OE,OD分别平分∠AOB和∠BOC,若∠AOB=90°,∠EOD=70°,求∠BOC的度数.
分析:根据角平分线的定义易得∠BOE的度数,那么根据∠EOD的度数,就能求得∠BOD的度数,根据角平分线定义可得到∠BOC的度数.
解答:解:∵OE,OD分别平分∠AOB和∠BOC,
∴∠EOB=
∠AOB=
×90°=45°,
又∵∠EOB+∠BOD=∠EOD=70°,
∴∠BOD=25°,
又∵∠BOC=2∠BOD,
∴∠BOC=2×25°=50°.
∴∠BOC的度数是50°
故答案为50°.
∴∠EOB=
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠EOB+∠BOD=∠EOD=70°,
∴∠BOD=25°,
又∵∠BOC=2∠BOD,
∴∠BOC=2×25°=50°.
∴∠BOC的度数是50°
故答案为50°.
点评:当告诉两角平分线的夹角的度数时,应从夹角入手,得到所求角的一半,进而求解.

练习册系列答案
相关题目
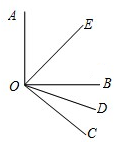 如图所示,OE,OD分别平分∠AOB和∠BOC,且∠AOB=90°;
如图所示,OE,OD分别平分∠AOB和∠BOC,且∠AOB=90°;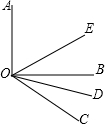 如图所示,OE,OD分别平分∠AOC和∠BOC.
如图所示,OE,OD分别平分∠AOC和∠BOC. 如图所示,OE,OD分别平分∠AOC和∠BOC,
如图所示,OE,OD分别平分∠AOC和∠BOC,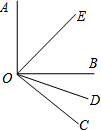 如图所示,OE和OD分别是∠AOB和∠BOC的平分线,且∠AOB=90°,∠BOC=40°,求∠EOD的度数.
如图所示,OE和OD分别是∠AOB和∠BOC的平分线,且∠AOB=90°,∠BOC=40°,求∠EOD的度数.