题目内容
如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠1=35º,那么∠2=______度.
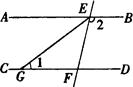

110°.
试题分析:根据两直线平行,内错角相等求出∠AEC=∠1,再根据角平分线的定义求出∠AEF的度数,然后根据平角的定义解答即可.
试题解析:∵AB∥CD,∠1=35°,
∴∠AEC=∠1=35°,
∵EG平分∠AEF,
∴∠AEF=2∠AEC=2×35°=70°,
∴∠2=180°-∠AEF=180°-70°=110°.
考点: 1.平行线的性质;2.角平分线的定义.

练习册系列答案
相关题目