��Ŀ����
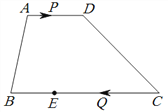
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���ABCDΪ�����Σ���֪��A����6��0����D����7��3������B��C�ڵڶ������ڣ�
��1�����B�����ꡣ
��2����������ABCD��ÿ��1����λ���ٶ���x������ƽ��t�룬������ijһʱ��t��ʹ�ڵ�һ�����ڵ�B��D����Ķ�Ӧ��B�䡢D����������ij������������ͼ���ϣ��������ʱt��ֵ�Լ���������������Ľ���ʽ��
��3���ڣ�2��������£����Ƿ����x���ϵĵ�P�ͷ���������ͼ���ϵĵ�Q��ʹ����P��Q��B�䡢D���ĸ���Ϊ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����������ĵ�P��Q�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��B����3��1����
��2��t��ֵΪ9����������������ʽΪy=![]() ��
��
��3����������ĵ�P��Q������ΪP��![]() ��0����Q��
��0����Q��![]() ��4����P��7��0����Q��3��2����
��4����P��7��0����Q��3��2����
����������1��������B����3��1��
�⣺��2���跴��������Ϊy=![]() ��
��
������ã���B������Ϊ����3+t��1������D������Ϊ����7+t��3����
�ߵ�B����D���ڸñ�������ͼ���ϣ�
��k=����3+t����1=����7+t����3��[��Դ:]
��ã�t=9��k=6��
�෴������������ʽΪy=![]() ��
��
(3) ��������ڣ����P������Ϊ��m��0������Q������Ϊ��n��![]() ����
����
��P��Q��B�䡢D���ĸ���Ϊ������ı�����ƽ���ı��η����������
�ٵ�B��D��Ϊ�Խ���ʱ�����߶�B��D�����е�ΪM����ͼ2��ʾ��

�ߵ�B�䣨6��1������D�䣨2��3������MΪ�߶�B��D�����е㣬
���M��������4��2����
�ߵ�M���߶�PQ���е㣬
�� ����ã�
����ã�![]() ��
��
��P��![]() ��0����Q��
��0����Q��![]() ��4����
��4����
�ڵ�B��D��Ϊ��ʱ��
���ı���PQB��D��Ϊƽ���ı��Σ�
�� ����ã�
����ã�![]() ��
��
��P��7��0����Q��3��2����
���Ͽ�֪������x���ϵĵ�P�ͷ���������ͼ���ϵĵ�Q��ʹ����P��Q��B�䡢D���ĸ���Ϊ������ı�����ƽ���ı��Σ���������ĵ�P��Q������ΪP��![]() ��0����Q��
��0����Q��![]() ��4����P��7��0����Q��3��2����
��4����P��7��0����Q��3��2����

 �������ϵ�д�
�������ϵ�д�