题目内容
【题目】按要求完成下列推理证明．
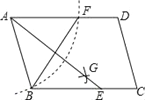
如图，已知点D为BC延长线上一点，CE∥AB．
求证：∠A+∠B+∠ACB＝180°
证明：∵CE∥AB，
∴∠1＝ ，（ ）
∠2＝ ，（ ）
又∠1+∠2+∠ACB＝180°（平角的定义），
∴∠A+∠B+∠ACB＝180°
【答案】∠B；两直线平行，同位角相等；∠A；两直线平行，内错角相等．
【解析】
根据平行线的性质得出∠1＝∠B，∠2＝∠A，即可得出答案．
证明：∵CE∥AB，
∴∠1＝∠B，（ 两直线平行，同位角相等）
∠2＝∠A，（两直线平行，内错角相等）
又∠1+∠2+∠ACB＝180°（平角的定义），
∴∠A+∠B+∠ACB＝180°，
故答案为：∠B；两直线平行，同位角相等；∠A；两直线平行，内错角相等．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
