Question

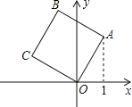
【题目】如图，将边长为2的正方形OABC放在平面直角坐标系中，O是原点，点A的横坐标为1，则点C的坐标为（　　）

A. （﹣2，1）B. （﹣1，2）C. （，﹣1）D. （﹣，1）

Answer 1

【答案】D

【解析】

首先过点C作CD⊥x轴于点D，过点A作AE⊥x轴于点E，易证得△AOE≌△OCD（AAS），则可得CD=OE=1，OD=AE=，继而求得答案．

解：过点C作CD⊥x轴于点D，过点A作AE⊥x轴于点E，

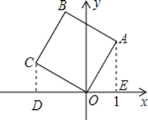
则∠ODC=∠AEO=90°，
∴∠OCD+∠COD=90°，
∵四边形OABC是正方形，
∴OC=OA，∠AOC=90°，
∴∠COD+∠AOE=90°，
∴∠OCD=∠AOE，
在△AOE和△OCD中，

，
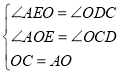∴△AOE≌△OCD（AAS），
∴CD=OE=1，OD=AE=，
∴点C的坐标为：（-，1）．
故选：D．