题目内容
直线y=x+1与x轴,y轴所围成的三角形面积为( )
| A、2 | ||
| B、1 | ||
C、
| ||
| D、3 |
分析:易得此直线与坐标轴的两个交点坐标,与坐标轴围成的三角形的面积=
×与x轴交点的横坐标的绝对值×与y轴交点的纵坐标.
| 1 |
| 2 |
解答:解:当x=0时,y=1,
当y=0时,x=-1,
∴所求三角形的面积=
×1×|-1|=
.
故选C.
当y=0时,x=-1,
∴所求三角形的面积=
| 1 |
| 2 |
| 1 |
| 2 |
故选C.
点评:本题考查了一次函数图象上点的坐标特征.某条直线与x轴,y轴围成三角形的面积为:
×直线与x轴的交点坐标的横坐标的绝对值×直线与y轴的交点坐标的纵坐标的绝对值.
| 1 |
| 2 |

练习册系列答案
相关题目
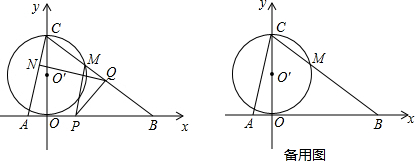
 (2012•兰州)如图,M为双曲线y=
(2012•兰州)如图,M为双曲线y=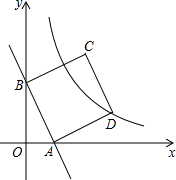 (2013•宛城区一模)如图,直线y=-2x+2与x轴y轴分别相交于点A、B,四边形ABCD是正方形,曲线y=
(2013•宛城区一模)如图,直线y=-2x+2与x轴y轴分别相交于点A、B,四边形ABCD是正方形,曲线y=