题目内容
在同一直角坐标系中，二次函数y=ax2+b与一次函数y=ax+b（a≠0）的图象可能是（ ）
分析：由于二次函数y=ax2+b与一次函数y=ax+b（a≠0）均过（0，b），可知正确答案从A、D中选，再根据二次函数的性质判断出a、b的值，然后根据a、b的值确定一次函数所过象限，从而选出正确答案．
解答：解：当x=0时，二次函数y=ax2+b与一次函数y=ax+b（a≠0）均有y=b，
可知函数均过（0，b），故B、C错误；
对于A、D：
A、二次函数y=ax2+b开口向上，a＞0，而一次函数过二、一、四象限，则a＜0，得出矛盾，故本选项错误；
D、二次函数y=ax2+b开口向上，a＜0，而一次函数过二、三、四象限，则a＜0，且二者均过（0，b）点，故本选项正确．
故选D．
可知函数均过（0，b），故B、C错误；
对于A、D：
A、二次函数y=ax2+b开口向上，a＞0，而一次函数过二、一、四象限，则a＜0，得出矛盾，故本选项错误；
D、二次函数y=ax2+b开口向上，a＜0，而一次函数过二、三、四象限，则a＜0，且二者均过（0，b）点，故本选项正确．
故选D．
点评：本题考查了二次函数的图象和一次函数的图象，要熟悉两函数的性质方可正确解答．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
相关题目
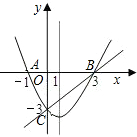如图，在同一直角坐标系中，二次函数的图象与两坐标轴分别交于A（-1，0）、点B（3，0）和点C（0，-3），一次函数的图象与抛物线交于B、C两点．
爱动脑筋的小明同学在买一双新的运动鞋时，发现了一些有趣现象，即鞋子的号码与鞋子的长（cm）之间存在着某种联系，经过收集数据，得到下表：