题目内容
【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A,B分别在射线OM,CN上,且∠C=∠OAB=108°,点E在线段CB上,OB平分∠AOE.
(1)图中有哪些与∠AOC相等的角?并说明理由;
(2)若平移AB,那么∠OBC与∠OEC的度数比是否随着AB位置变化而变化?若变化,找出变化规律;若不变,求出这个比值.
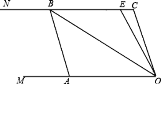
【答案】(1)∠ABC和∠BAM,理由见解析;(2)1:2.
【解析】
(1)根据平行线的性质和角的关系解答即可;
(2)根据平行线的性质和角平分线的定义解答即可.
(1)∵OM∥CN,∴∠AOC=180°-∠C=180°-108°=72°,
∠ABC=180°-∠OAB=180°-108°=72°.
又∵∠BAM=180°-∠OAB=180°-108°=72°,
∴与∠AOC相等的角是∠ABC和∠BAM.
(2)∵OM∥CN,∴∠OBC=∠AOB,∠OEC=∠AOE.
∵OB平分∠AOE, ∴∠AOE=2∠AOB.
∴∠OEC=2∠OBC. ∴∠OBC:∠OEC=1:2.

练习册系列答案
相关题目




