��Ŀ����
����Ŀ�����꼶һ�չ�ˡ���һ�����顱�Ļ����ί���ѧ���Ķ��鼮������������ʾ����飬�ʾ������ˡ�С˵������Ϸ�硱����ɢ�ġ�����������
�ĸ����ÿλͬѧ��ѡһ����ݵ����������˲�������Ƶ���ֲ���������ͳ��ͼ������ͼ���ṩ����Ϣ���ش��������⣺
��� | Ƶ���������� | Ƶ�� |
С˵ | 0.5 | |
Ϸ�� | 4 | |
ɢ�� | 10 | 0.25 |
���� | 6 | |
�ϼ� | m | 1 |
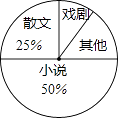
��1������m=��
��2��������ͳ��ͼ�У�������������ռ�İٷֱ�Ϊ��
��3���ڵ����ʾ��У��ס��ҡ���������λͬѧѡ���ˡ�Ϸ�硱�࣬�ִ�������ѡ��2��ͬѧ�μ�ѧУ��Ϸ�����ţ����û���״ͼ���б��ķ�������ѡȡ��2��ǡ�����Һͱ��ĸ��ʣ�
���𰸡�
��1��40
��2��15%
��3���⣺����״ͼ����ͼ��ʾ��
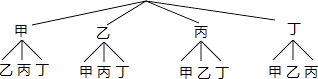
���еȿ��ܵ������12�֣�����ǡ���DZ����ҵ������2�֣�
��P�������ң�= ![]() =
= ![]()
���������⣺��1����ϲ��ɢ�ĵ���10�ˣ�Ƶ��Ϊ0.25��
��m=10��0.25=40��2��������ͳ��ͼ�У�������������ռ�İٷֱ�Ϊ ![]() ��100%=15%��
��100%=15%��
�ʴ�Ϊ��15%��
��1������ϲ��ɢ����������Ƶ�ʣ����ɵó�m��ֵ��
��2���á������������������40���������ռ�ٷֱȡ�
��3���������ڲ��Żأ��г���״ͼ��������еȿ�������ǡ���DZ����ҵ�����Ŀ����������ݸ��ʹ�ʽ������⡣

����Ŀ��ij���½���һ����ҵ��ÿ�½�����1960����ˮ��Ϊ��������������ҵ�ƻ�������ˮ���������������������ͺ���ѡ��
��ˮ�������ͺ� | A�� | B�� |
������ˮ��������/�£� | 240 | 180 |
��֪�̼��۳���2̨A�͡�3̨B����ˮ���������ܼ�Ϊ44��Ԫ���۳���1̨A�͡�4̨B����ˮ���������ܼ�Ϊ42��Ԫ��
��1����ÿ̨A�͡�B����ˮ�������ļ۸�
��2��Ϊȷ����ÿ�²�������ˮȫ�������꣬����ҵ����������������ˮ����������ô��������Ҫ֧������Ǯ��