题目内容
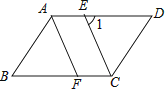
【题目】如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.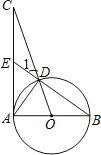
(1)求证:∠1=∠CAD;
(2)若AE=EC=2,求⊙O的半径.
【答案】
(1)
证明:∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠ADO+∠BDO=90°,
∵AC为⊙O的切线,
∴OA⊥AC,
∴∠OAD+∠CAD=90°,
∵OA=OD,
∴∠OAD=∠ODA,
∵∠1=∠BDO,
∴∠1=∠CAD;
(2)
解:∵∠1=∠CAD,∠C=∠C,
∴△CAD∽△CDE,
∴CD:CA=CE:CD,
∴CD2=CACE,
∵AE=EC=2,
∴AC=AE+EC=4,
∴CD=2 ![]() ,
,
设⊙O的半径为x,则OA=OD=x,
则Rt△AOC中,OA2+AC2=OC2,
∴x2+42=(2 ![]() +x)2,
+x)2,
解得:x= ![]() .
.
∴⊙O的半径为 ![]()
【解析】(1)由AB为⊙O的直径,AC为⊙O的切线,易证得∠CAD=∠BDO,继而证得结论;(2)由(1)易证得△CAD∽△CDE,然后由相似三角形的对应边成比例,求得CD的长,再利用勾股定理,求得答案.此题考查了切线的性质、圆周角定理以及相似三角形的判定与性质.注意证得△CAD∽△CDE是解此题的关键.
【考点精析】认真审题,首先需要了解圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半),还要掌握切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)的相关知识才是答题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目