Question

【题目】△ABC和△ECD都是等边三角形

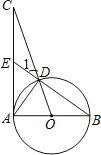
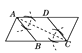
（1）如图1，若B、C、D三点在一条直线上，求证：BE=AD；

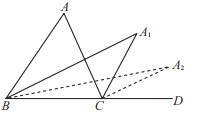
（2）保持△ABC不动，将△ECD绕点C顺时针旋转，使∠ACE=90°（如图2），BC与DE有怎样的位置关系？说明理由．

Answer 1

【答案】（1）证明见解析；（2）BC垂直平分DE，理由见解析.

【解析】

试题（1）利用等边三角形的性质和已知条件证明△ACD≌△BCE即可；

（2）BC垂直平分DE，延长BC交DE于M，证明∠ECM=∠DCM，利用三线合一证明即可．

试题解析：∵△ABC和△ECD都是等边三角形，∴AC=BC，EC=DC，∠ACB=∠ECD=60°.

∴∠ACB+∠ACE=∠ECD+∠ACE，即∠ACD=∠BCE.

∴△ACD≌△BCE. ∴AD=BE.

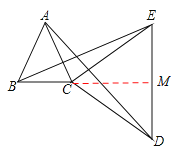
（2）BC垂直平分DE，理由如下：

如图，延长BC交DE于M，

∵∠ACB=60°，∠ACE=90°，∴∠ECM=180°-∠ACB-∠ACE=30°.

∵∠DCM=∠ECD-∠ECM=30°，∴∠ECM=∠DCM.

∵△ECD是等边三角形，∴CM垂直平分DE，即BC垂直平分DE．