题目内容
【题目】已知：如图， 
， 
， 
， 
在同一直线上，且 
， 
， 
.求证：四边形 
是平行四边形.
【答案】解：连接 
， 
， 
,如图所示：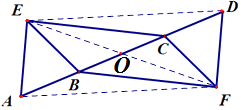
∵ 
， 
.
∴四边形 
为平行四边形；
∴ 
， 
；
又∵ 
∴ 
∴ 
；
又∵
∴四边形 
是平行四边形.
方法二：
采用全等三角形证明，证出 
；
得到： 
；
得到： 
，或者通过全等得到 
；
∴四边形 是平行四边形.
【解析】连接 AF 、 ED 、 EF ,如图.由 AE=DF ， AE∥DF 得到四边形 AEDF 为平行四边形；由平行四边形的性质得EO=FO ，AO=DO ；
由等量代换得 BO=CO ；再由EO=FO，根据对角线互相平分的四边形为平行四边形.
【考点精析】关于本题考查的平行四边形的判定与性质，需要了解若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积才能得出正确答案．
练习册系列答案
相关题目
【题目】下表是初二年级50名同龄女生身高数据：
身高/cm | 146 | 151 | 153 | 154 | 156 | 157 | 158 | 159 | 160 |
人数 | 1 | 2 | 2 | 2 | 3 | 4 | 8 | 4 | 4 |
身高/cm | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 169 | |
人数 | 2 | 4 | 3 | 2 | 3 | 4 | 1 | 1 |
（1）根据下表的分组方法进行数据整理，补全频数分布表：
（2）根据分布表画出频数分布直方图．
（3）观察频数分布表和频数分布直方图回答问题：为了参加广播操比赛，老师打算从以上50名女生中挑选30名队员。为了让参赛队员的身高比较整齐，老师应该选择身高在什么范围内的同学呢？请写出答案并简述理由．
