题目内容
【题目】如果关于
的一元二次方程
有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”，研究发现了此类方程的一般性结论：设其中一根为
，则另一个根为
，因此
，所以有
；我们记“
”即
时，方程为倍根方程；
下面我们根据此结论来解决问题：
（1）方程①
；方程②
；方程③
这几个方程中，是倍根方程的是_________（填序号即可）；
（2）若
是倍根方程，则
的值为______；
【答案】（1）①、③；（2）
或
【解析】
（1）根据“倍根方程”的定义，找出方程①、②、③中K的值，由此即可得出结论；
（2）将方程（x1）（mx-n）＝0整理成一般式，再根据“倍根方程”的定义，当K＝0，整理后即可得出
的值；
解：（1）①∵
∴
=(-3)2-
×2×1=0
∴①是倍根方程；
②
∴=
∴②不是倍根方程；
③
，
∴=12-×1×
=0
∴③是倍根方程；
故答案为：①、③；
（2）∵
是倍根方程，
∴
∴=
解得：
或
∴或
故答案为：或
练习册系列答案
相关题目
【题目】有这样一个问题：探究函数
的图象与性质．小华根据学习函数的经验，对函数的图象与性质进行了探究．下面是小华的探究过程，请补充完整：
(1)函数的自变量x的取值范围是___________；
(2)下表是y与x的几组对应值．m的值为_______；
x | -2 |
| -1 |
|
|
| 1 | 2 | 3 | 4 | … |
y | 0 |
| m |
|
|
|
| 1 |
|
| … |
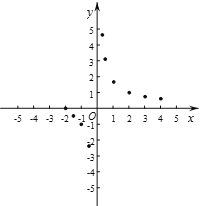
(3)如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
(4)结合函数的图象，写出该函数的一条性质：____________．
(5)结合函数图象估计
的解的个数为_______个．
