题目内容
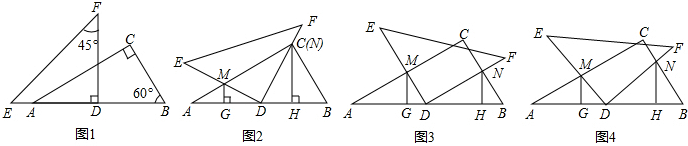
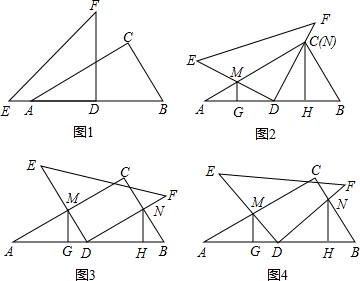
已知:将一副三角板(Rt△ABC和Rt△DEF)如图①摆放,点E、A、D、B在一条直线上,且D是AB中点,将Rt△DEF绕着点D顺时针方向旋转角α(0°<α<90°),在旋转过程中,直线DE、AC相交于点M,直线DF、BC相交于点N,分别过点M、N作直线AB的垂线,垂足为G、H.(1)猜想:在旋转过程中,AG与DH的数量关系是:______;
(2)就旋转角α的情况,请选择图②、③、④中的一种情况,对你的猜想进行证明.
友情提示:若选择图②(即α=30°时),满分为8分;若选择图③(即α=60°时),满分为10分;选择图④(即任意情况0°<α<90°时).

【答案】分析:(1)相等,根据等腰三角形的性质推出DH= BD,AG=
BD,AG= AD即可;
AD即可;
(2)求出∠AMD=90°=∠CMD,得出矩形CMDN,推出∠DNB=90°,根据直角推出∠MDA=∠B,∠A=∠NDB,根据AAS证△ADM和△DBN全等,推出AM=DN,根据AAS证△AGM和△DHN全等即可.
解答:解:(1)AG和DH的数量关系是相等,
理由是:如图2,∵∠ACB=90°,∠A=30°,D为AB中点,
∴∠B=60°,CD=BD=AD,
∴△CDB是等边三角形,
∴∠CDB=60°,CD=BD=BC,
∵CH⊥AB,
∴DH=BH= DB,
DB,
∵∠EDF=90°,
∴∠MDA+∠CDB=90°,
∴∠MDA=90°-60°=30°=∠A,
∴AM=MD,
∵MG⊥AD,
∴AG=GD= AD,
AD,
∵AD=BD,
∴AG=DH.
故答案为:相等.
(2)结论是AG=DH,
证明:选图3,
∵∠A=30°,∠EDA=α=60°,
∴∠AMD=90°=∠CMD,
∵∠C=∠EDF=90°,
∴四边形CMDN是矩形,
∴∠CND=90°=∠DNB,
∵∠A=30°,∠ACB=90°,
∴∠B=60°=∠EDA,
∵∠EDF=90°,
∴∠NDB=180°-90°-60°=30°=∠A,
在△AMD和△DNB中
 ,
,
∴△AMD≌△DNB,
∴AM=DN,
∵MG⊥AB,NH⊥AB,
∴∠MGA=∠NHD=90°,
在△AGM和△DHN中
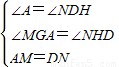 ,
,
∴△AGM≌△DHN,
∴AG=DH.
选④
证明:∵在Rt△AMG中,∠A=30°,
∴∠AMG=60°=∠B,
∵∠AGM=∠BHN=90°,
∴△AGM∽△NHB,
∴ =
= ①,
①,
∵∠MDG=α,
∴∠DMG=90°-α=∠NDH,
∵∠MGD=∠DHN=90°,
∴△MGD∽△DHN,
∴ =
= ②,
②,
①×②得: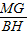 •
•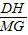 =
= •
• ,
,
 =
= ,
,
 =
= ,
,
∴由比例性质得: =
= ,
,
即 =
=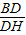 ,
,
∵AD=BD,
∴AG=DH.
点评:本题综合考查了全等三角形的性质和判定的运用,解此题的关键是找出两个全等的三角形,根据三角形全等的性质推出结论.题型较好,有一定的规律性.
 BD,AG=
BD,AG= AD即可;
AD即可;(2)求出∠AMD=90°=∠CMD,得出矩形CMDN,推出∠DNB=90°,根据直角推出∠MDA=∠B,∠A=∠NDB,根据AAS证△ADM和△DBN全等,推出AM=DN,根据AAS证△AGM和△DHN全等即可.
解答:解:(1)AG和DH的数量关系是相等,
理由是:如图2,∵∠ACB=90°,∠A=30°,D为AB中点,
∴∠B=60°,CD=BD=AD,
∴△CDB是等边三角形,
∴∠CDB=60°,CD=BD=BC,
∵CH⊥AB,
∴DH=BH=
 DB,
DB,∵∠EDF=90°,
∴∠MDA+∠CDB=90°,
∴∠MDA=90°-60°=30°=∠A,
∴AM=MD,
∵MG⊥AD,
∴AG=GD=
 AD,
AD,∵AD=BD,
∴AG=DH.
故答案为:相等.
(2)结论是AG=DH,
证明:选图3,
∵∠A=30°,∠EDA=α=60°,
∴∠AMD=90°=∠CMD,
∵∠C=∠EDF=90°,
∴四边形CMDN是矩形,
∴∠CND=90°=∠DNB,
∵∠A=30°,∠ACB=90°,
∴∠B=60°=∠EDA,
∵∠EDF=90°,
∴∠NDB=180°-90°-60°=30°=∠A,
在△AMD和△DNB中
 ,
,∴△AMD≌△DNB,
∴AM=DN,
∵MG⊥AB,NH⊥AB,
∴∠MGA=∠NHD=90°,
在△AGM和△DHN中
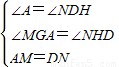 ,
,∴△AGM≌△DHN,
∴AG=DH.
选④
证明:∵在Rt△AMG中,∠A=30°,
∴∠AMG=60°=∠B,
∵∠AGM=∠BHN=90°,
∴△AGM∽△NHB,
∴
 =
= ①,
①,∵∠MDG=α,
∴∠DMG=90°-α=∠NDH,
∵∠MGD=∠DHN=90°,
∴△MGD∽△DHN,
∴
 =
= ②,
②,①×②得:
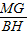 •
•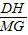 =
= •
• ,
, =
= ,
, =
= ,
,∴由比例性质得:
 =
= ,
,即
 =
=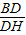 ,
,∵AD=BD,
∴AG=DH.
点评:本题综合考查了全等三角形的性质和判定的运用,解此题的关键是找出两个全等的三角形,根据三角形全等的性质推出结论.题型较好,有一定的规律性.

练习册系列答案
相关题目