题目内容
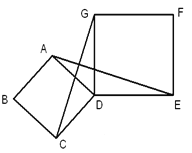
【题目】如图所示,四边形ABCD、DEFG都是正方形,连接AE、CG。
(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想。
【答案】(1)证明见解析(2)垂直关系
【解析】
试题分析:可以把结论涉及的线段放到△ADE和△CDG中,考虑证明全等的条件,又有两个正方形,∴AD=CD,DE=DG,它们的夹角都是∠ADG加上直角,故夹角相等,可以证明全等;再利用互余关系可以证明AE⊥CG.
试题解析:(1)如图,
∵AD=CD,DE=DG,∠ADC=∠GDE=90°,
又∵∠CDG=90°+∠ADG=∠ADE,
∴△ADE≌△CDG(SAS).
∴AE=CG.
(2)猜想:AE⊥CG.
理由:如图,设AE与CG交点为M,AD与CG交点为N.
∵△ADE≌△CDG,
∴∠DAE=∠DCG.
又∵∠ANM=∠CND,
∴△AMN∽△CDN.
∴∠AMN=∠ADC=90°.
∴AE⊥CG.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

